题目内容
如图,已知在平面直角坐标系中,四边形ABCO是梯形,且BC∥AO,其中A(6,0),B(3, ),∠AOC=60°,动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P,Q运动的时间为t(秒).
),∠AOC=60°,动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P,Q运动的时间为t(秒).


(1)求点C的坐标及梯形ABCO的面积;
(2)当点Q在CO边上运动时,求△OPQ的面积S与运动时间t的函数关系式,并写出自变量t的取值范围;
(3)以O,P,Q为顶点的三角形能构成直角三角形吗?若能,请求出t的值;若不能,请说明理由.
 ),∠AOC=60°,动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P,Q运动的时间为t(秒).
),∠AOC=60°,动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P,Q运动的时间为t(秒).

(1)求点C的坐标及梯形ABCO的面积;
(2)当点Q在CO边上运动时,求△OPQ的面积S与运动时间t的函数关系式,并写出自变量t的取值范围;
(3)以O,P,Q为顶点的三角形能构成直角三角形吗?若能,请求出t的值;若不能,请说明理由.
(1) (2)
(2)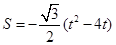 (
(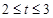 ) (3)当t=1或t=2时,△OPQ为直角三角形
) (3)当t=1或t=2时,△OPQ为直角三角形
 (2)
(2)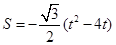 (
(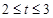 ) (3)当t=1或t=2时,△OPQ为直角三角形
) (3)当t=1或t=2时,△OPQ为直角三角形试题分析:(1)作CM⊥OA于点M,知CM
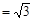 ,由∠AOC=60°易求BM=1,求出C点坐标;由B点坐标可求BC的长,从而梯形面积可求;
,由∠AOC=60°易求BM=1,求出C点坐标;由B点坐标可求BC的长,从而梯形面积可求;(2)用含有t的代数式分别表示△OPQ的高和底,求出△OPQ的的面积即可表示出S与运动时间t的函数关系式;
(3)分点Q分别在边BC、OC、OA上运动时进行讨论,即可求出t的值.
试题解析:(1)作CM⊥OA于点M,
∵∠AOC=60°,∴∠OCM=30°,
∵B(3,
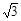 ),BC∥AO,∴CM
),BC∥AO,∴CM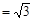 ,
,设OM=
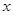 ,则OC=
,则OC=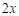 ,∴
,∴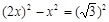
解得
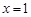 ,∴OM=1,OC=2,
,∴OM=1,OC=2,∴C(1,
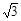 ),
),∵B(3,
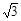 ),∴BC=2,
),∴BC=2,∵A(6,0),∴OA=6,
∴
 ,
,(2)如图1,当动点Q运动到OC边时,OQ=
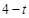 ,
,作QG⊥OP,∴∠OQG=30°,
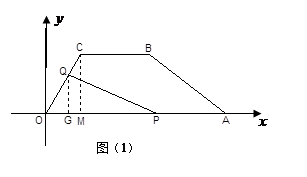
∴
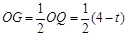 ,∴
,∴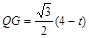 ,
,又∵OP=2t,
∴
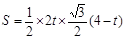
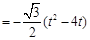 (
(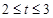 );
);(3)根据题意得出:
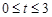 ,
,当
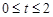 时,Q在BC边上运动,延长BC交y轴于点D,
时,Q在BC边上运动,延长BC交y轴于点D,此时OP=2t,
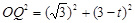 ,
,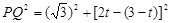 ,
,∵∠POQ<∠POC=60°,
∴若△OPQ为直角三角形,只能是∠OPQ=90°或∠OQP=90°,
若∠OPQ=90°,如图2,则∠PQD=90°,
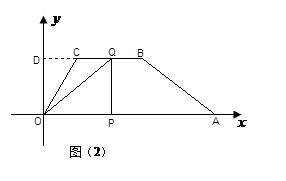
∴四边形PQDO为矩形,
∴OP=QD,∴2t=3-t,
解得t=1,
若∠OQP=90°,如图3,则OQ2+PQ2=PO2,
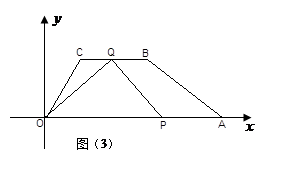
即
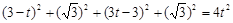 ,
,解得:t1=t2=2,
当
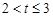 时,Q在OC边上运动,
时,Q在OC边上运动,若∠OQP=90°,
∵∠POQ=60°,∴∠OPQ=30°,
∴
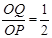 ,
,若∠OPQ=90°,同理:
 ,
,而此时OP=2t>4,OQ<OC=2,
∴
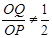 ,
,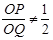 ,
,故当Q在OC边上运动时,△OPQ不可能为直角三角形,
综上所述,当t=1或t=2时,△OPQ为直角三角形。
考点: 1.二次函数;2.直角三角形的判定.

练习册系列答案
相关题目
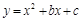 与x轴交于A、B两点(点A在点B的左侧),点B的坐标为
与x轴交于A、B两点(点A在点B的左侧),点B的坐标为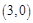 ,与y轴交于点
,与y轴交于点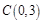 ,顶点为D。
,顶点为D。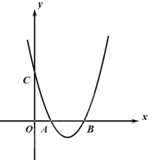
 中,O是坐标原点,抛物线
中,O是坐标原点,抛物线 与x轴交与A,B两点(点A在点B的左侧),与y轴相交与点C,如果点M在y轴右侧的抛物线上,
与x轴交与A,B两点(点A在点B的左侧),与y轴相交与点C,如果点M在y轴右侧的抛物线上, ,那么点M的坐标是 。
,那么点M的坐标是 。
 上一动点,连结AE、OE,问在抛物线上是否存在一点M,使∠MOA︰∠AEO=2︰3,若存在,试求出点M的坐标;若不存在,试说明理由.
上一动点,连结AE、OE,问在抛物线上是否存在一点M,使∠MOA︰∠AEO=2︰3,若存在,试求出点M的坐标;若不存在,试说明理由. x+k=0有两个不相等的实数根,则k的取值范围是 _________ .
x+k=0有两个不相等的实数根,则k的取值范围是 _________ . x2+3共有的性质是
x2+3共有的性质是 和
和 的关系说法中,正确的是( )
的关系说法中,正确的是( ) 轴对称;
轴对称; ,
, )既在抛物线
)既在抛物线 的最小值是 .
的最小值是 .