题目内容

已知圆锥的底面半径为r=20cm，高h= $数学公式$ cm，现在有一只蚂蚁从底边上一点A出发．在侧面上爬行一周又回到A点，求蚂蚁爬行的最短距离．

解：设扇形的圆心角为n，圆锥的顶为E，
∵r=20cm，h=20 $\text{[math]}$ cm
∴由勾股定理可得母线l= $\text{[math]}$ =80cm，
而圆锥侧面展开后的扇形的弧长为2×20π= $\text{[math]}$ ，
∴n=90°
即△EAA′是等腰直角三角形，
∴由勾股定理得：AA'= 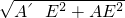$\text{[math]}$ =80 $\text{[math]}$ cm．
答：蚂蚁爬行的最短距离为80 $\text{[math]}$ cm．
分析：蚂蚁爬行的最短距离是圆锥的展开图的扇形中AA′的长度．根据勾股定理求得母线长后，利用弧长等于底面周长求得扇形的圆心角的度数为90度，再由等腰直角三角形的性质求解．
点评：本题利用了勾股定理，弧长公式，圆的周长公式，等腰直角三角形的性质求解．