题目内容
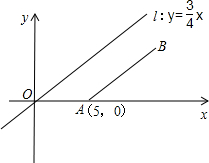 已知A(5,0),点B在第一象限内,并且AB与直线l:
已知A(5,0),点B在第一象限内,并且AB与直线l: 平行,AB长为8.
平行,AB长为8.
(1)求点B的坐标.
(2)点P是直线l: 上的动点,求△PAB内切圆的最大面积.
上的动点,求△PAB内切圆的最大面积.
解:(1)∵AB与直线l: 平行,
平行,
∴设直线AB的解析式为: +b,
+b,
∵A(5,0),
∴0= ×5+b,
×5+b,
解得:b=- ,
,
∴直线AB的解析式为:y=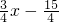 ,
,
设B点的坐标为:(x0,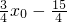 ),
),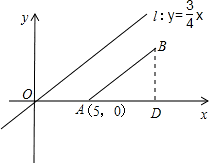
作BD⊥x轴于D点,
∴BD=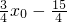
AD=x0-5,
∵AB长为8.
∴(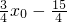 )2+(x0-5)2=82,
)2+(x0-5)2=82,
解得:x0=- (不合题意舍去)或
(不合题意舍去)或 ,
,
∴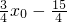 =4.8,
=4.8,
∴点B的坐标为:(11.4,4.8)
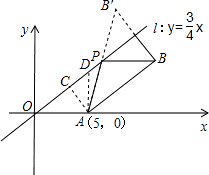
(2)过A点作DA⊥x轴交直线L与D点,作AC⊥OD于C点,
∵点C、D在直线l: 上,
上,
∴AC:CO=3:4,
∵OA=5,
∴AC=3,
∴S△PAB= AB•AC=
AB•AC= ×8×3=12,
×8×3=12,
∴r=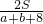 ,
,
∵△PAB周长最小时,r最大,
∴过B作点B关于直线l的对称点B′,则BB′=3×2=6,
∴AB′=10,
a+b+8=18,
∴最大r=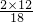 =
= ,
,
∴△PAB内切圆的最大面积为: π.
π.
分析:(1)首先求得直线AB的解析式,然后设出B点的坐标构造直角三角形并利用勾股定理得到有关B点的坐标的方程,求得B点的坐标即可;
(2)根据AB=8,以及直线l和点A的位置,求出三角形ABP的面积,利用三角形与内切圆关系是:r=(2×三角形面积)÷三角形周长(a+b+8),再根据a+b>8找r的最大值后求得最大面积即可.
点评:本题考查了一次函数的综合知识及三角形的内切圆的半径与三边和面积之间的关系,是一道综合性较强的题目.
 平行,
平行,∴设直线AB的解析式为:
 +b,
+b,∵A(5,0),
∴0=
 ×5+b,
×5+b,解得:b=-
 ,
,∴直线AB的解析式为:y=
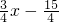 ,
,设B点的坐标为:(x0,
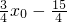 ),
),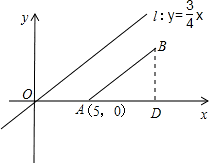
作BD⊥x轴于D点,
∴BD=
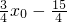
AD=x0-5,
∵AB长为8.
∴(
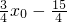 )2+(x0-5)2=82,
)2+(x0-5)2=82,解得:x0=-
 (不合题意舍去)或
(不合题意舍去)或 ,
,∴
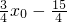 =4.8,
=4.8,∴点B的坐标为:(11.4,4.8)

(2)过A点作DA⊥x轴交直线L与D点,作AC⊥OD于C点,
∵点C、D在直线l:
 上,
上,∴AC:CO=3:4,
∵OA=5,
∴AC=3,
∴S△PAB=
 AB•AC=
AB•AC= ×8×3=12,
×8×3=12,∴r=
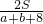 ,
,∵△PAB周长最小时,r最大,
∴过B作点B关于直线l的对称点B′,则BB′=3×2=6,
∴AB′=10,
a+b+8=18,
∴最大r=
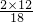 =
= ,
,∴△PAB内切圆的最大面积为:
 π.
π.分析:(1)首先求得直线AB的解析式,然后设出B点的坐标构造直角三角形并利用勾股定理得到有关B点的坐标的方程,求得B点的坐标即可;
(2)根据AB=8,以及直线l和点A的位置,求出三角形ABP的面积,利用三角形与内切圆关系是:r=(2×三角形面积)÷三角形周长(a+b+8),再根据a+b>8找r的最大值后求得最大面积即可.
点评:本题考查了一次函数的综合知识及三角形的内切圆的半径与三边和面积之间的关系,是一道综合性较强的题目.

练习册系列答案
相关题目

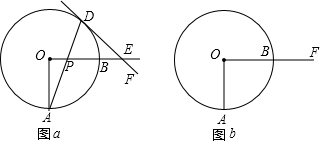
 18、已知三角形ABC.
18、已知三角形ABC. (1)画出△ABC关于点O的中心对称图形△DEF.
(1)画出△ABC关于点O的中心对称图形△DEF.