Question

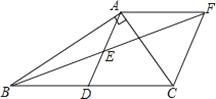
【题目】如图，BD是△ABC的角平分线，它的垂直平分线分别交AB，BD，BC于点E，F，G，连接ED，DG．

（1）请判断四边形EBGD的形状，并说明理由；
（2）若∠ABC=30°，∠C=45°，ED=2 ，点H是BD上的一个动点，求HG+HC的最小值．

Answer 1

【答案】
（1）

解：四边形EBGD是菱形．

理由：∵EG垂直平分BD，

∴EB=ED，GB=GD，

∴∠EBD=∠EDB，

∵∠EBD=∠DBC，

∴∠EDF=∠GBF，

在△EFD和△GFB中，

，

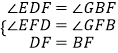∴△EFD≌△GFB，

∴ED=BG，

∴BE=ED=DG=GB，

∴四边形EBGD是菱形

（2）

解：作EM⊥BC于M，DN⊥BC于N，连接EC交BD于点H，此时HG+HC最小，

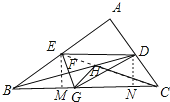
在RT△EBM中，∵∠EMB=90°，∠EBM=30°，EB=ED=2 ，

∴EM= BE= ，

∵DE∥BC，EM⊥BC，DN⊥BC，

∴EM∥DN，EM=DN= ，MN=DE=2 ，

在RT△DNC中，∵∠DNC=90°，∠DCN=45°，

∴∠NDC=∠NCD=45°，

∴DN=NC= ，

∴MC=3 ，

在RT△EMC中，∵∠EMC=90°，EM= ．MC=3 ，

∴EC= = =10 ．

∵HG+HC=EH+HC=EC，

∴HG+HC的最小值为10

【解析】（1）结论四边形EBGD是菱形．只要证明BE=ED=DG=GB即可．（2）作EM⊥BC于M，DN⊥BC于N，连接EC交BD于点H，此时HG+HC最小，在RT△EMC中，求出EM、MC即可解决问题．本题考查平行四边形的判定和性质、菱形的判定和性质、角平分线的性质、垂直平分线的性质、勾股定理等知识，解题的关键是利用对称找到点H的位置，属于中考常考题型．
【考点精析】根据题目的已知条件，利用角平分线的性质定理和平行四边形的判定与性质的相关知识可以得到问题的答案，需要掌握定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上；若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积．