题目内容
如图，E为□ABCD边AD的中点，连接CE、BD交于点F，若△DEF的面积为1，则△BCF的面积为________．
4
分析：平行四边形的对边平行，从而可得到△EFD，△CFB是相似三角形，从而根据面积比等于相似比的平方，从而得解．
解答：∵AD∥BC，
∴△EFD∽△CFB，
∵E为□ABCD边AD的中点，
∴
=
=
，
∵△DEF的面积为1，
∴△BCF的面积为4．
故答案为：4．
点评：本题考查平行四边形的性质，相似三角形的判定和性质．
分析：平行四边形的对边平行，从而可得到△EFD，△CFB是相似三角形，从而根据面积比等于相似比的平方，从而得解．
解答：∵AD∥BC，
∴△EFD∽△CFB，
∵E为□ABCD边AD的中点，
∴
==，∵△DEF的面积为1，
∴△BCF的面积为4．
故答案为：4．
点评：本题考查平行四边形的性质，相似三角形的判定和性质．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
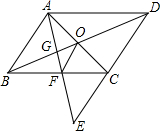已知：如图，E为?ABCD中DC边的延长线上一点，且CE=DC，连接AE，分别交BC、BD于点F、G，连接AC交BD于O，连接OF，判断AB与OF的位置关系和大小关系，并证明你的结论．
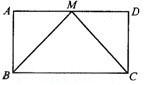34、已知：如图，M为?ABCD的AD边上的中点，且MB=MC，
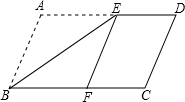如图，E为?ABCD中AD边上的一点，将△ABE沿BE折叠使得点A刚好落在BC边上的F点处，若AB为4，ED为3，则?ABCD的周长为
如图，E为?ABCD的边BC延长线上一点，AE与BD交于点F，与DC交于点G．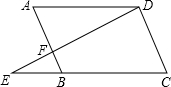
如图，E为?ABCD的边CB的延长线上一点，DE交AB于点F，则图中与△ADF相似的三角形是