题目内容

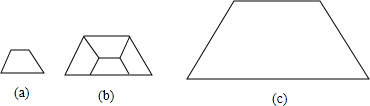
图（a）、（b）、（c）都是上底与腰长相等，下底是腰长的两倍的等腰梯形．图（a）的腰长是1，图（b）的腰长是2，则图（b）可以分割成4个图（a）的等腰梯形．
（1）若图（c）的腰长是4，则图（c）可以分割成个图（a）的等腰梯形；
（2）若图（c）的腰长是64，则图（c）可以分割成个图（a）的等腰梯形．

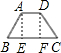解：（1）分别过A，D点作AE⊥BC于E，DF⊥BC于F．
∵上底与腰长相等，下底是腰长的两倍的等腰梯形．图（a）的腰长是1，
∴AB=1，BC=2，BE= $\text{[math]}$ ，AE= $\text{[math]}$ ，
∴图（a）的面积为：（1+2）× $\text{[math]}$ ÷2= $\text{[math]}$ ，
若图（c）的腰长是4，同理可得图（c）的面积为：（4+8）×2 $\text{[math]}$ ÷2=12 $\text{[math]}$ ，
∵12 $\text{[math]}$ ÷ $\text{[math]}$ =16，
∴图（c）可以分割成16个图（a）的等腰梯形；

（2）若图（c）的腰长是64，同理可得图（c）的面积为：（64+128）×32 $\text{[math]}$ ÷2=3072 $\text{[math]}$ ，
∵3072 $\text{[math]}$ ÷ $\text{[math]}$ =4096，
∴图（c）可以分割成4096个图（a）的等腰梯形．
故答案为：16；4096．
分析：（1）先求出（a）的高，根据梯形的面积公式求得（a）的面积，同理求得腰长是4的图（c）面积，相除即可求解；
（2）由（1）可知（a）的面积，同理求得腰长是64的图（c）面积，相除即可求解．
点评：本题考查了等腰梯形，本题关键是求得等腰梯形的高，熟练掌握梯形的面积公式：S= $\text{[math]}$ （a+b）h．