题目内容
 (2013•聊城)如图,一只猫头鹰蹲在一棵树AC的B(点B在AC上)处,发现一只老鼠躲进短墙DF的另一侧,猫头鹰的视线被短墙遮住,为了寻找这只老鼠,它又飞至树顶C处,已知短墙高DF=4米,短墙底部D与树的底部A的距离为2.7米,猫头鹰从C点观测F点的俯角为53°,老鼠躲藏处M(点M在DE上)距D点3米.
(2013•聊城)如图,一只猫头鹰蹲在一棵树AC的B(点B在AC上)处,发现一只老鼠躲进短墙DF的另一侧,猫头鹰的视线被短墙遮住,为了寻找这只老鼠,它又飞至树顶C处,已知短墙高DF=4米,短墙底部D与树的底部A的距离为2.7米,猫头鹰从C点观测F点的俯角为53°,老鼠躲藏处M(点M在DE上)距D点3米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(1)猫头鹰飞至C处后,能否看到这只老鼠?为什么?
(2)要捕捉到这只老鼠,猫头鹰至少要飞多少米(精确到0.1米)?
分析:(1)根据猫头鹰从C点观测F点的俯角为53°,可知∠DFG=90°-53°=37°,在△DFG中,已知DF的长度,求出DG的长度,若DG>3,则看不见老鼠,若DG<3,则可以看见老鼠;
(2)根据(1)求出的DG长度,求出AG的长度,然后在Rt△CAG中,根据
=sin∠C=sin37°,即可求出CG的长度.
(2)根据(1)求出的DG长度,求出AG的长度,然后在Rt△CAG中,根据
| AG |
| CG |
解答:解:(1)能看到;
由题意得,∠DFG=90°-53°=37°,
则
=tan∠DFG,
∵DF=4米,
∴DG=4×tan37°≈4×0.75=3(米),
故能看到这只老鼠;
(2)由(1)得,AG=AD+DG=2.7+3=5.7(米),
又
=sin∠C=sin37°,
则CG=
≈
=9.5(米).
答:要捕捉到这只老鼠,猫头鹰至少要飞约9.5米.
由题意得,∠DFG=90°-53°=37°,
则
| DG |
| DF |
∵DF=4米,
∴DG=4×tan37°≈4×0.75=3(米),
故能看到这只老鼠;
(2)由(1)得,AG=AD+DG=2.7+3=5.7(米),
又
| AG |
| CG |
则CG=
| AG |
| sin37° |
| 5.7 |
| 0.60 |
答:要捕捉到这只老鼠,猫头鹰至少要飞约9.5米.
点评:本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形并解直角三角形,利用三角函数求解相关线段,难度一般.

练习册系列答案
相关题目
 (2013•聊城)如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为
(2013•聊城)如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为 (2013•聊城)如图,D是△ABC的边BC上一点,已知AB=4,AD=2.∠DAC=∠B,若△ABD的面积为a,则△ACD的面积为( )
(2013•聊城)如图,D是△ABC的边BC上一点,已知AB=4,AD=2.∠DAC=∠B,若△ABD的面积为a,则△ACD的面积为( )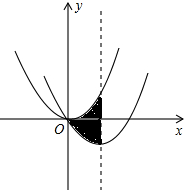 (2013•聊城)如图,在平面直角坐标系中,抛物线y=
(2013•聊城)如图,在平面直角坐标系中,抛物线y=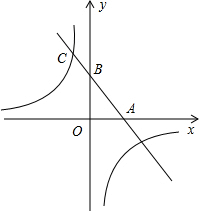 (2013•聊城)如图,一次函数的图象与x轴,y轴分别相交于A,B两点,且与反比例函数y=
(2013•聊城)如图,一次函数的图象与x轴,y轴分别相交于A,B两点,且与反比例函数y=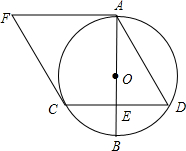 (2013•聊城)如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=
(2013•聊城)如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=