Question

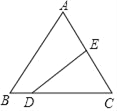
【题目】如图，等边△ABC的边长为8，D、E两点分别从顶点B、C出发，沿边BC、CA以1个单位/s、2个单位/s的速度向顶点C、A运动，DE的垂直平分线交BC边于F点，若某时刻tan∠CDE= 时，则线段CF的长度为_____．

Answer 1

【答案】2

【解析】解：作EH⊥BC于H，设线段DE的垂直平分线交DE于G．

∵△ABC是等边三角形，∴∠C=60°．在Rt△EHC中，EC=2t，∴CH=t，EH=2t．在Rt△DEH中，∵tan∠CDE==，∴DH=4t．∵BD=t，BC=8，∴t+4t+t=8，∴t=，∴DH=，EH=，CH=．∵GF垂直平分线段DE，∴DF=EF，设DF=EF=x．在Rt△EFH中，∵EF2=EH2+FH2，∴x2=（）2+（﹣x）2，解得：x=，∴CF=﹣+=2．故答案为：2．