题目内容
【题目】如图,将一块三角板和半圆形量角器按图中方式叠放,三角板一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧( ![]() )对应的圆心角(∠AOB)为120°,OC的长为2cm,则三角板和量角器重叠部分的面积为 .
)对应的圆心角(∠AOB)为120°,OC的长为2cm,则三角板和量角器重叠部分的面积为 . 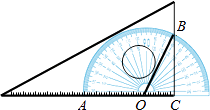
【答案】![]() +2
+2 ![]() (cm2)
(cm2)
【解析】解:∵∠AOB=120°, ∴∠BOC=60°,
在Rt△OBC中,OC=2cm,∠BOC=60°,
∴∠OBC=30°,
∴OB=4cm,BC=2 ![]() cm,
cm,
则S扇形OAB= ![]() =
= ![]() (cm2),S△OBC=
(cm2),S△OBC= ![]() OC×BC=2
OC×BC=2 ![]() (cm2),
(cm2),
故S重叠=S扇形OAB+S△OBC= ![]() +2
+2 ![]() (cm2)
(cm2)
所以答案是: ![]() +2
+2 ![]() (cm2).
(cm2).
【考点精析】本题主要考查了扇形面积计算公式的相关知识点,需要掌握在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能正确解答此题.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目