Question

已知抛物线的顶点是C (0，a) (a>0，a为常数)，并经过点(2a，2a)，点D（0，2a）为一定点.
(1)求含有常数a的抛物线的解析式；
(2)设点P是抛物线任意一点，过P作PH⊥x轴，垂足是H，求证：PD = PH；
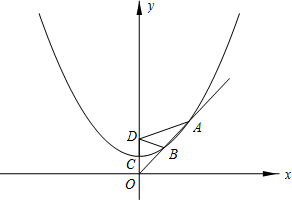
(3)设过原点O的直线l与抛物线在第一象限相交于A、B两点，若DA=2DB，且S_△ABD = 4，求a的值.

 

Answer 1

解：（1）设抛物线的解析式为y=kx²+a                     (1分)
∵点D（2a，2a）在抛物线上，
4a²k+a = 2a    ∴k =                         (3分)
∴抛物线的解析式为y= x²+a                 （4分）
（2）设抛物线上一点P（x，y），过P作PH⊥x轴，PG⊥y轴，在Rt△GDP中，
由勾股定理得：PD²=DG²+PG²=(y–2a)²+x² =y² – 4ay+4a²+x²    
                                                           (5分) 
∵y= x²+a ∴x² = 4a´ (y– a)= 4ay– 4a²     (6分)
∴PD ²= y²– 4ay+4a² +4ay– 4a²= y² =PH²
∴PD = PH 
（3）过B点BE ⊥x轴，AF⊥x轴.
由（2）的结论：BE=DB AF=DA
∵DA=2DB ∴AF=2BE ∴AO = 2BO
∴B是OA的中点，
∴C是OD的中点，
连结BC
∴BC= = = BE = DB                 (9分)
过B作BR⊥y轴，
∵BR⊥CD  ∴CR=DR，OR= a + = ，
∴B点的纵坐标是，又点B在抛物线上，
∴ = x²+a  ∴x² =2a²
∵x>0     ∴x = a
∴B (a， )                          (10分)
AO = 2OB，∴S_△ABD=S_△OBD = 4
所以，´2a´a= 4
∴a²=" 4  " ∵a>0 ∴a =" 2              " (12分)

解析