题目内容

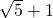E为平行四边形ABCD的边AD延长线上一点，且为AE的黄金分割点，即AD= $数学公式$ AE，BE交DC于点F，已知AB= $数学公式$ ，则CF的长是________．

2
分析：根据题意作出草图，先证明△ABE和△DFE相似，根据相似三角形对应边成比例求出DF的长度，又平行四边形对边相等，CD=AB，然后即可求出CF的长度．
解答：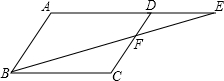

解：在平行四边形ABCD中，AB=CD，AB∥CD，
∴△ABE∽△DFE，
∴ $\text{[math]}$ = $\text{[math]}$ ，
∵AD= $\text{[math]}$ AE，
∴ $\text{[math]}$ =1- $\text{[math]}$ = $\text{[math]}$ ，
∴DF= $\text{[math]}$ ×（ $\text{[math]}$ +1）= $\text{[math]}$ -1，
∴CF=（ $\text{[math]}$ +1）-（ $\text{[math]}$ -1）=2．
故答案为：2．
点评：本题主要考查了黄金分割的知识，利用平行四边形的性质证明三角形相似，再利用相似三角形对应边成比例列出比例式是解题的关键，难度不大．

练习册系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

如图，△ABC中，∠C=90°，AC=4，BC=3．半径为1的圆的圆心P以1个单位/s的速度由点A沿AC方向在AC上移动，设移动时间为t（单位：s）．
（1）当t为何值时，⊙P与AB相切；
（2）作PD⊥AC交AB于点D，如果⊙P和线段BC交于点E，证明：

s时，四边形PDBE为平行四边形．

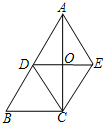23、如图，已知在Rt△ABC中，∠C=90°，点O为边AC的中点，点D为边AB上一点，过点C作AB的平行线，交DO的延长线于点E．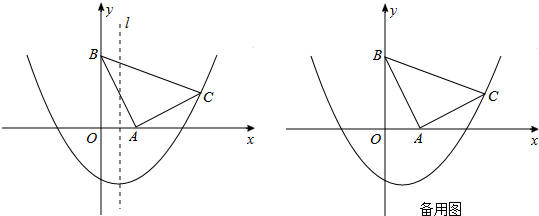
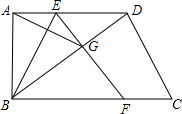（1）证明：四边形ADCE为平行四边形；
（2）当四边形ADCE为怎样的四边形时，AD=BD，并加以证明．

（2013•湘潭）如图，在坐标系xOy中，△ABC是等腰直角三角形，∠BAC=90°，A（1，0），B（0，2），抛物线y=

x²+bx-2的图象过C点．
（1）求抛物线的解析式；
（2）平移该抛物线的对称轴所在直线l．当l移动到何处时，恰好将△ABC的面积分为相等的两部分？
（3）点P是抛物线上一动点，是否存在点P，使四边形PACB为平行四边形？若存在，求出P点坐标；若不存在，说明理由．

（2012•宜昌）如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°．点E为底AD上一点，将△ABE沿直线

BE折叠，点A落在梯形对角线BD上的G处，EG的延长线交直线BC于点F．
（1）点E可以是AD的中点吗？为什么？
（2）求证：△ABG∽△BFE；
（3）设AD=a，AB=b，BC=c
①当四边形EFCD为平行四边形时，求a，b，c应满足的关系；
②在①的条件下，当b=2时，a的值是唯一的，求∠C的度数．

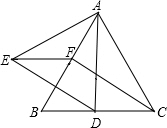已知：如图，在等边△ABC中，D、F分别为CB、BA上的点，且CD=BF，以AD为边作等边三角形ADE．求证：
（1）△ACD≌△CBF；
（2）四边形CDEF为平行四边形．