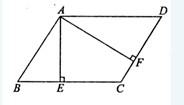
题目内容
已知在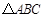 中,
中,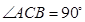 ,
, ,
,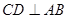 于
于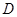 ,点
,点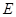 在直线
在直线 上,
上,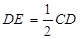 ,点
,点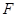 在线段
在线段 上,
上,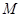 是
是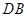 的中点,直线
的中点,直线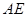 与直线
与直线 交于
交于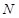 点.
点.
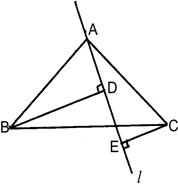
(1)如图1,若点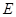 在线段
在线段 上,请分别写出线段
上,请分别写出线段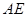 和
和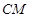 之间的位置关系和数量关系:___________,___________;
之间的位置关系和数量关系:___________,___________;
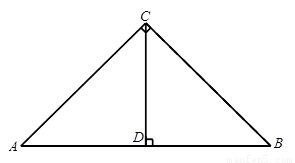

(2)在(1)的条件下,当点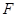 在线段
在线段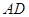 上,且
上,且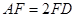 时,求证:
时,求证: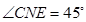 ;
;
(3)当点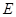 在线段
在线段 的延长线上时,在线段
的延长线上时,在线段 上是否存在点
上是否存在点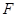 ,使得
,使得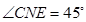 .若存在,请直接写出
.若存在,请直接写出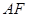 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
【答案】
【解析】
试题分析:(1)有已给条件可猜想线段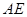 和
和 之间的位置关系和数量关系是:
之间的位置关系和数量关系是: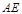 ⊥
⊥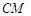 ,
,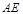 =
=
(2)如图,过点A作AG⊥AB,且AG=BM,,连接CG、FG,延长AE交CM于H.
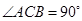 ,
,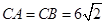
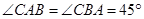 ,
,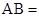
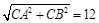 ,
,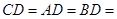
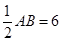 从而证得
从而证得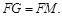 △
△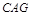 和△
和△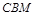 全等;
全等;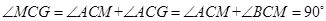 ,再证得△
,再证得△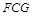 和△
和△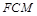 全等,得到
全等,得到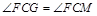 ,从而得
,从而得 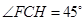 ,
,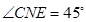 .
.
(3)点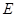 在线段
在线段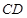 的延长线上时,在线段
的延长线上时,在线段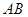 上存在点
上存在点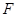 ,使得
,使得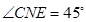 . 这时
. 这时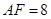
试题解析:(1)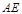 ⊥
⊥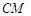 ,
,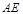 =
= .
.
(2)如图,过点A作AG⊥AB,且AG=BM,,连接CG、FG,延长AE交CM于H.
∵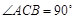 ,
,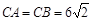 ,
,
∴∠CAB=∠CBA=45°,AB= .
.
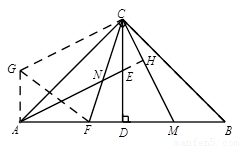
∴∠GAC=∠MBC=45°.
∵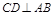 ,
,
∴CD=AD=BD=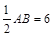 .
.
∵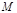 是
是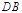 的中点,
的中点,
∴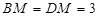 .
.
∴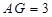 .
.
∵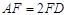 ,
,
∴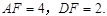
∴
∵AG⊥AF,
∴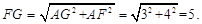
∴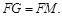
在△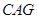 和△
和△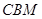 中,
中,
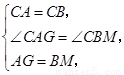
∴△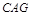 ≌△
≌△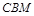 .
.
∴
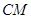
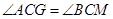 .
.
∴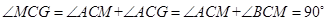 .
.
在△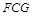 和△
和△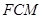 中,
中,
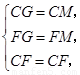
∴△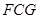 ≌△
≌△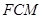 .
.
∴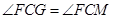 .
.
∴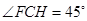 .
.
由(1)知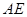 ⊥
⊥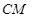 ,
,
∴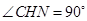
∴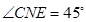 .
.
(3)存在. 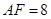
考点:1.勾股定理,2.全等三角形的判定和性质,

练习册系列答案
相关题目
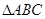 中,
中, =90°,
=90°, 是过
是过 点的直线,
点的直线, 交直线于点
交直线于点 交直线于点
交直线于点 .
.
 ≌
≌ .
. ,求
,求 的长.
的长.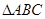 中,
中,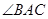 =90°,
=90°,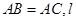 是过
是过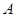 点的直线,
点的直线,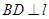 交直线于点
交直线于点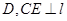 交直线于点
交直线于点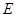 .
.
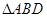 ≌
≌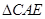 .
.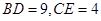 ,求
,求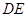 的长.
的长.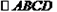 中, AE⊥BC于点E, AF⊥CD于点F,若∠EAF=60°, BE =2 cm,FD= 3 cm,求AB、BC的长和
中, AE⊥BC于点E, AF⊥CD于点F,若∠EAF=60°, BE =2 cm,FD= 3 cm,求AB、BC的长和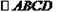 的面积.
的面积.