题目内容
x、y、z为实数且x+y+z= ,则x+y+z=________.
,则x+y+z=________.
28
分析:将已知等式配方为几个非负数的和为0的形式,可求x、y、z的值.
解答:已知等式可化为
(x-3)-4 +4+(y-6)-2
+4+(y-6)-2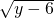 +1+(z-5)-6
+1+(z-5)-6 +9=0,
+9=0,
配方,得( -2)2+(
-2)2+(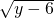 -1)2+(
-1)2+( -3)2=0,
-3)2=0,
∴ -2=0,
-2=0,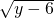 -1=0,
-1=0, -3=0,
-3=0,
解得x=7,y=7,z=14,
∴x+y+z=28.
故答案为:28.
点评:本题考查了配方法在等式变形中的运用.关键是利用完全平方公式将等式配方成几个非负数的和为0的形式,利用非负数的性质解题.
分析:将已知等式配方为几个非负数的和为0的形式,可求x、y、z的值.
解答:已知等式可化为
(x-3)-4
 +4+(y-6)-2
+4+(y-6)-2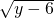 +1+(z-5)-6
+1+(z-5)-6 +9=0,
+9=0,配方,得(
 -2)2+(
-2)2+(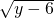 -1)2+(
-1)2+( -3)2=0,
-3)2=0,∴
 -2=0,
-2=0,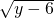 -1=0,
-1=0, -3=0,
-3=0,解得x=7,y=7,z=14,
∴x+y+z=28.
故答案为:28.
点评:本题考查了配方法在等式变形中的运用.关键是利用完全平方公式将等式配方成几个非负数的和为0的形式,利用非负数的性质解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目