题目内容
如图,在长方形ABCD中,AB=2,BC=4,Q是DC边的中点,P为一动点,若点P从B点出发,以1个单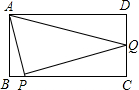 位/秒的速度沿着B→C方向运动.设从点B出发运动了x秒,
位/秒的速度沿着B→C方向运动.设从点B出发运动了x秒,(1)写出△AQP的面积y关于x的函数关系式.并求出自变量x的取值范围;
(2)问当x取何值时,△AQP是等腰三角形?
分析:(1)将△AQP的面积转化为长方形ABCD的面积与其余三个三角形的面积的差;
(2)先确定△AQP是等腰三角形时P点的位置,根据位置求x的值.
(2)先确定△AQP是等腰三角形时P点的位置,根据位置求x的值.
解答: 解:(1)y=4×2-
解:(1)y=4×2-
×2x-4×1×
-4×
×1=4-
,(0≤x≤4).
(2)①当P位于P1时,有(AP1)2=(QP1)2,
根据勾股定理得:22+x2=(4-x)2+12,解得x=
;
②当P位于B时,为等腰三角形,此时x=0;
③当P位于P2时,有(AP2)2=(QA)2,根据勾股定理得:42+12=x2+22,解得x=
.
当x为0秒或
秒或
秒时,△AQP是等腰三角形.
 解:(1)y=4×2-
解:(1)y=4×2-| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
(2)①当P位于P1时,有(AP1)2=(QP1)2,
根据勾股定理得:22+x2=(4-x)2+12,解得x=
| 13 |
| 8 |
②当P位于B时,为等腰三角形,此时x=0;
③当P位于P2时,有(AP2)2=(QA)2,根据勾股定理得:42+12=x2+22,解得x=
| 13 |
当x为0秒或
| 13 |
| 8 |
| 13 |
点评:本题是一个动点问题,考查了对函数概念的理解以及如何将图形的变化转化为函数问题.题目将图形和函数有机结合,体现了数形结合思想在数学中的重要作用.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
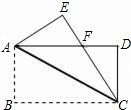 于点F.
于点F. 如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.
如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.

