题目内容
如图,已知反比例函数 =
= 的图像与一次函数
的图像与一次函数 =
= +
+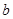 的图像交于两点A(-2,1)、B(
的图像交于两点A(-2,1)、B(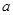 ,-2).
,-2).
(1)求反比例函数和一次函数的解析式;
(2)若一次函数 =
= +
+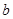 的图像与
的图像与 轴交于点C,求△AOC(O为坐标原点)的面积.
轴交于点C,求△AOC(O为坐标原点)的面积.
(1) 1=
1=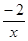 ,
, 2=-
2=-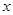 -1;(2)1
-1;(2)1
解析试题分析:(1)将A(-2,1)代入 1=
1=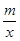 即可求得反比例函数的解析式,从而可求得点B的坐标,再根据待定系数法即可求的一次函数的解析式;
即可求得反比例函数的解析式,从而可求得点B的坐标,再根据待定系数法即可求的一次函数的解析式;
(2)先求得一次函数的图象与坐标轴的交点C的坐标,再根据三角形的面积公式求解即可.
(1)将A(-2,1)代入 1=
1=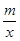 得1=
得1=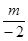 ,
,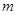 =-2
=-2
又B(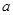 ,-2)在
,-2)在 1=
1=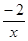 上,即-2=
上,即-2=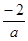 ,
,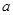 =1
=1
∵ 2=
2=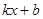 过点A(-2,1),B(1,-2)
过点A(-2,1),B(1,-2)
∴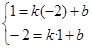 ,解得
,解得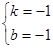
∴ 1=-
1=-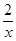 ,
, 2=-
2=-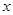 -1;
-1;
(2)令 2=-
2=-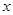 -1中
-1中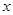 =0,得
=0,得 2=-1,C(0,-1)
2=-1,C(0,-1)
设A到 轴距离为d=∣- 2∣=2
轴距离为d=∣- 2∣=2
∴S△AOC=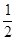 ∣OC∣·d=
∣OC∣·d=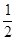 ×1×2=1.
×1×2=1.
考点:反比例函数和一次函数的图象的交点问题
点评:此类问题是初中数学的重点,在中考中比较常见,一般难度不大,需熟练掌握.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y= 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y=