题目内容
(本题满分9分)
如图,以为顶点的抛物线与
轴交于点
.已知
、
两点坐标分别为(3,0)、(0,4).
(1)求抛物线的解析式;
(2)设是抛物线上的一点(
、
为正整数),且它位于对称轴的右侧.若以
、
、
、
为顶点的四边形四条边的长度是四个连续的正整数,求点
的坐标;
(3)在(2)的条件下,试问:对于抛物线对称轴上的任意一点,
![]() 是否总成立?请说明理由.
是否总成立?请说明理由.
(1)
(2)(6,4)
(3)![]() 总是成立
总是成立
解析:(1)设,把
代入,得
.
∴.
(2)∵为正整数,
,
∴应该是9的倍数.
∴是3 的倍数.
又∵,
∴…
当时,
,此时,
.
∴四边形的四边长为3,4,5,6.
当时,
,
∴四边形的四边长不能是四个连续的正整数.
∴点坐标只有一种可能(6,4).
(3) 设,
与对称轴交点为
.
则.
.
∴=
.
∴当时,
有最小值,
∴![]() 总是成立.
总是成立.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
.(本题满分5分)如图一根木棒放在数轴上,木棒的左端与数轴上的点A重合,右端与点B重合.
 |
1.若将木棒沿数轴向右水平移动,则当它的左端移动到B点时,它的右端在数轴上所对应的数为20;若将木棒沿数轴向左水平移动,则当它的右端移动到A点时,则它的左端在数轴上所对应的数为5(单位:cm),由此可得到木棒长为 cm.
2.由题(1)的启发,请你借助“数轴”这个工具帮助小红解决下列问题:
问题:一天,小红去问曾当过数学老师现在退休在家的爷爷的年龄,爷爷说:“我若是你现在这么大,你还要40年才出生;你若是我现在这么大,我已经125岁,是老寿星了,哈哈!”,请求出爷爷现在多少岁了?

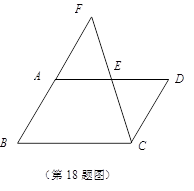

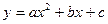 交
交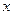 轴于
轴于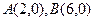 两点,交
两点,交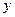 轴于点
轴于点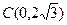 .
.
 (2)若此抛物线的对称轴与直线
(2)若此抛物线的对称轴与直线 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交