题目内容
如图，AD为△ABC的中线，且AB=13，BC=10，AD=12，则AC等于
- A.10
- B.11
- C.12
- D.13
D
分析：先利用中线的性质得到BD=5，再根据勾股定理的逆定理，得到△ABD为直角三角形，进而得到AC的值．
解答：∵AD为△ABC的中线，
∴BD=5，
∴BD2+AD2=AB2，
∴三角形ADB为直角三角形，
∵∠ADB为直角，
∴△ABD≌△ADC，
∴AC=AB=13．
故选D．
点评：本题是一道综合题，需要学生把中线的性质和勾股定理结合起来求解．
分析：先利用中线的性质得到BD=5，再根据勾股定理的逆定理，得到△ABD为直角三角形，进而得到AC的值．
解答：∵AD为△ABC的中线，
∴BD=5，
∴BD2+AD2=AB2，
∴三角形ADB为直角三角形，
∵∠ADB为直角，
∴△ABD≌△ADC，
∴AC=AB=13．
故选D．
点评：本题是一道综合题，需要学生把中线的性质和勾股定理结合起来求解．
练习册系列答案
相关题目
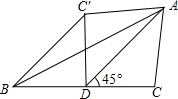如图，AD为△ABC的中线，∠ADC=45°，把△ADC沿AD对折，点C落在点C′的位置，BC=4，求BC′的长．
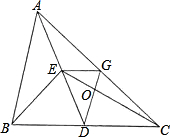如图，AD为△ABC的中线，BE为△ABD的中线．
如图，AD为△ABC的中线，BE为三角形ABD中线，
如图，AD为△ABC的中线，BE为△ABD的中线．
如图，AD为△ABC的中线，BE为△ABD的中线．