题目内容
 已知△BDE和△ABC都是等边三角形,DE交AB于点F.若BD=1,∠CBD=45°,求△BEF的面积.
已知△BDE和△ABC都是等边三角形,DE交AB于点F.若BD=1,∠CBD=45°,求△BEF的面积.
 解:过点F作FH⊥BE于点H,
解:过点F作FH⊥BE于点H,∵△BDE和△ABC都是等边三角形,∠CBD=45°,
∴∠EBF=45°,∠E=60°,
设EH=x,
在Rt△EFH中,∠E=60°,
∴FH=
 x,
x,在Rt△BFH中,∠EBF=45°,
∴HB=FH=
 x,
x,∵EH+HB=EB=1,
∴x+
 x=1,
x=1,解得:x=
 ,
,∴S△BEF=
 BE•FH=
BE•FH= x=
x=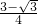 .
.分析:首先过点F作FH⊥BE于点H,由△BDE和△ABC都是等边三角形,∠CBD=45°,易得∠EBF=45°,∠E=60°,然后设EH=x,利用三角函数的知识,即可表示出FH,HB的长,继而得方程:x+
 x=1,解此方程即可求得答案.
x=1,解此方程即可求得答案.点评:此题考查了等边三角形的性质以及三角函数等知识.此题难度适中,注意掌握辅助线的作法,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
相关题目
 22、填空,完成下列证明过程.
22、填空,完成下列证明过程.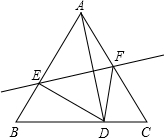 作AD的垂直平分线分别与边AB、AC交于点E、F.
作AD的垂直平分线分别与边AB、AC交于点E、F.
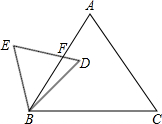 已知△BDE和△ABC都是等边三角形,DE交AB于点F.若BD=1,∠CBD=45°,求△BEF的面积.
已知△BDE和△ABC都是等边三角形,DE交AB于点F.若BD=1,∠CBD=45°,求△BEF的面积.