题目内容
在△ABC中,A(3,0),B(0,4),C(0,0).
(Ⅰ)已知AB的长可能是4,4,5,5,5,5,试通过测量或者估算,写出你认为正确的那个值(只须写出结果);
(Ⅱ)设P是△ABC内一点,且到三边的距离相等,试求点P的坐标(要写出过程);
(Ⅲ)坐标平面上到直线AB,BC,CA等距离的点一共有多少个?它们分别在哪些象限?如果第四象限存在满足条件的点,试求出它的坐标.(前两问只须写出结果,第三问要写出过程)
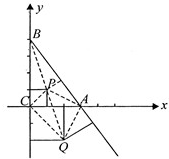 解:(Ⅰ)根据A(3,0),B(0,4),可以只计测量得出答案;
解:(Ⅰ)根据A(3,0),B(0,4),可以只计测量得出答案;也可以利用勾股定理求出:AB=5;
(Ⅱ)由于点P在第一象限,且到两坐标轴的距离相等,则设P(a,b),
则S△PAB+S△PBC+S△PCA=S△ABC=6,
即5a+4a+3a=12,所以a=1,故所求点P的坐标为(1,1).
(Ⅲ)一共有4个点,除上述P点外,还有三点,它们分别在第一象限,第二象限,第四象限.
显然,第四象限的点可设为Q(b,-b),其中b>0.
由于S△QAB+S△QBC-S△QCA=S△ABC=6,所以5b+4b-3b=12,b=2,
故所求点Q的坐标为(2,-2).
分析:(1)根据A(3,0),B(0,4),可以只计测量得出答案;
(2)可以利用三角形面积分割求出P点的坐标;
(3)根据三角形面积S△QAB+S△QBC-S△QCA=S△ABC=6求出第四象限存在满足条件的点的坐标即可.
点评:此题主要考查了一次函数的综合应用以及三角形面积分割法求内切圆半径,此题难度不大比较典型.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
在△ABC中,∠C=90°,BC=12,AB=13,则tanA的值是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,a=
,b=
,c=2
,则最大边上的中线长为( )
| 2 |
| 6 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、以上都不对 |
 23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
 18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于
18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于