题目内容
【题目】如图,在正方形ABCD中,AB=4,AC与BD交于点O, N是AO的中点,点M在BC边上,且BM=3, P为对角线BD上一点,当对角线BD平分∠NPM时,PM-PN值为( )

A.1B.![]() C.2D.
C.2D.![]()
【答案】A
【解析】
作以BD为对称轴作N的对称点N',连接PN',MN',依据PM-PN=PM-PN'≤MN',可得当P,M,N'三点共线时,PM-PN'= MN',再求得![]() ,即可得出PM∥AB∥CD,∠CMN'=90°,再根据△N'CM为等腰直角三角形,即可得到CM=MN'=1,即PM-PN=1.
,即可得出PM∥AB∥CD,∠CMN'=90°,再根据△N'CM为等腰直角三角形,即可得到CM=MN'=1,即PM-PN=1.
解:如图所示,作以BD为对称轴作N的对称点N',连接PN',MN',
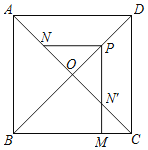
根据轴对称性质可知,PN=PN',
∴PM-PN=PM-PN'≤MN',
当P,M,N'三点共线时,PM-PN'= MN',
∵正方形边长为4,
∴AC=![]() AB=4
AB=4![]() ,
,
∵O为AC中点,
∴AO=OC=2![]() ,
,
∵N为OA中点,
∴ON=![]() ,
,
∴ON'=CN'=![]() ,
,
∴AN'=3![]() ,
,
∵BM=3,
∴CM=AB-BM=4-3=1,
∴![]()
∴PM∥AB∥CD,∠CMN'=90°,
∵∠N'CM=45°,
∴△N'CM为等腰直角三角形,
∴CM=MN'=1,
即PM-PN=1,
故选:A

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
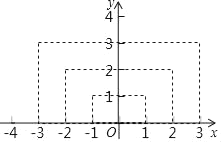
【题目】已知y是x的函数,x的取值范围为任意实数,如图是x与y的几组对应值,小华同学根据研究函数的己有经验探素这个函数的有关性质,并完成下列问题.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 3 | 2 | 1 | 0 | 1 | 2 | 3 | … |
(1)如图,小华在平面直角坐标系中描出了上述几组值对应的点,请你根据描出的点画出函数的图象;
(2)请根据你画出的函数图象,完成
①当x=﹣4时,求y的值;
②当2012≤|y|≤2019时,求x的取值范围.