题目内容
 如图,矩形ABCD,AB=2,AD=3,点P为AD上一点,PE⊥PC,交AB于E点,点Q在AP上不与P点重合,且QE⊥QC,
如图,矩形ABCD,AB=2,AD=3,点P为AD上一点,PE⊥PC,交AB于E点,点Q在AP上不与P点重合,且QE⊥QC,
(1)求证:AP•DP=AE•DC;
(2)求AP+AQ的值.
(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,∠A=∠D=90°,
∵PE⊥PC,
∴∠EPC=90°,
∴∠AEP+∠APE=90°,∠APE+∠DPC=90°,
∴∠AEP=∠DPC,
∵∠A=∠D,
∴△AEP∽△DPC,
∴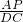 =
=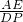 ,
,
∴AP•DP=AE•DC.

(2)解:连接CE,取CE中点F,过F作FG∥CD交AD于G,
∵AB∥CD,∠A=90°,
∴AE∥FG∥CD,
∴AG=DG AD=
AD= ,FG⊥AD,
,FG⊥AD,
∵QE⊥CE,PE⊥PC,
∴∠EQC=∠EPC=90°,
∵F为CE中点,
∴QF= CE,PF=
CE,PF= CE,
CE,
∴QF=PF,
∵FG⊥AD,
∴QG=PG,
∴AP+AQ=AG+GP+AG-GQ=2AG=2× =3.
=3.
分析:(1)求出∠A=∠D,∠AEP=∠DPC,证出△AEP∽△DPC即可.
(2)连接CE,取CE中点F,过F作FG∥CD交AD于G,求出AG=DG,求出QF=PF,根据等腰三角形性质得出QG=PG,即可得出答案.
点评:本题考查了矩形性质,直角三角形斜边上中线性质,平行线分线段成比例定理,相似三角形的性质和判定的应用,主要考查学生综合运用定理进行推理和计算的能力.
∴AB∥CD,∠A=∠D=90°,
∵PE⊥PC,
∴∠EPC=90°,
∴∠AEP+∠APE=90°,∠APE+∠DPC=90°,
∴∠AEP=∠DPC,
∵∠A=∠D,
∴△AEP∽△DPC,
∴
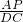 =
=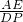 ,
,∴AP•DP=AE•DC.

(2)解:连接CE,取CE中点F,过F作FG∥CD交AD于G,
∵AB∥CD,∠A=90°,
∴AE∥FG∥CD,
∴AG=DG
 AD=
AD= ,FG⊥AD,
,FG⊥AD,∵QE⊥CE,PE⊥PC,
∴∠EQC=∠EPC=90°,
∵F为CE中点,
∴QF=
 CE,PF=
CE,PF= CE,
CE,∴QF=PF,
∵FG⊥AD,
∴QG=PG,
∴AP+AQ=AG+GP+AG-GQ=2AG=2×
 =3.
=3.分析:(1)求出∠A=∠D,∠AEP=∠DPC,证出△AEP∽△DPC即可.
(2)连接CE,取CE中点F,过F作FG∥CD交AD于G,求出AG=DG,求出QF=PF,根据等腰三角形性质得出QG=PG,即可得出答案.
点评:本题考查了矩形性质,直角三角形斜边上中线性质,平行线分线段成比例定理,相似三角形的性质和判定的应用,主要考查学生综合运用定理进行推理和计算的能力.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 17、已知,如图,矩形ABCD中,AC与BD相交于点O,BE⊥AC于E,CF⊥BD于F.
17、已知,如图,矩形ABCD中,AC与BD相交于点O,BE⊥AC于E,CF⊥BD于F.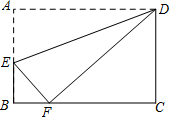 (2012•武汉)如图,矩形ABCD中,点E在边AB上,将矩形ABCD沿直线DE折叠,点A恰好落在边BC的点F处.若AE=5,BF=3,则CD的长是( )
(2012•武汉)如图,矩形ABCD中,点E在边AB上,将矩形ABCD沿直线DE折叠,点A恰好落在边BC的点F处.若AE=5,BF=3,则CD的长是( )
 Q的面积为y(cm2).
Q的面积为y(cm2). 如图,矩形ABCD的边AB、BC的长分别为
如图,矩形ABCD的边AB、BC的长分别为