题目内容
 如图,四边形ABCD为一梯形纸片,AB∥CD,AD=BC.翻折纸片ABCD,使点A与点C重合,折痕为EF.连接CE、CF、BD,AC、BD的交点为O,若CE⊥AB,AB=7,CD=3.下列结论中:①AC=BD,②EF∥BD,③S四边形AECF=AC•EF,④EF=
如图,四边形ABCD为一梯形纸片,AB∥CD,AD=BC.翻折纸片ABCD,使点A与点C重合,折痕为EF.连接CE、CF、BD,AC、BD的交点为O,若CE⊥AB,AB=7,CD=3.下列结论中:①AC=BD,②EF∥BD,③S四边形AECF=AC•EF,④EF= ,⑤连接F0;则F0∥AB.正确的序号是________.
,⑤连接F0;则F0∥AB.正确的序号是________.
①②④
分析:根据等腰梯形的特点和对角线互相垂直的四边形的面积=对角线积的一半的知识来判断.
解答:∵四边形ABCD为等腰梯形,∴∠A=∠B∵AD=BC,AB=AB,
∴△ADB≌△BCA,∴AC=DB,①正确;
∵CE⊥AB∴∠AEF=45°,由翻折得到EF⊥AC,∴∠CAB=45°由全等得到∠OBA=∠OAB=45°,∴∠OBA=∠AEF=45°那么EF∥BD,②对;
∠S四边形AECF= ×AC•EF,③错;
×AC•EF,③错;
易得BE=(7-3)÷2=2,CE=AE=5,做FM⊥AB于点M,
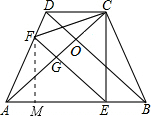
∴CE:BE=FM:AM,∵FM=ME,∴AM=5-x,解得x= ,那么EF=
,那么EF= ④正确;
④正确;
OG=OA-AG= -
-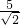 =
= ,FG=
,FG= -
- 易得OG≠FG,那么∠FOG≠45°,∴⑤错.
易得OG≠FG,那么∠FOG≠45°,∴⑤错.
正确的序号是①②④.
点评:注意使用等腰梯形中的三角形全等,以及常用的辅助线方法,对角线互相垂直的四边形的面积=对角线积的一半等知识.
分析:根据等腰梯形的特点和对角线互相垂直的四边形的面积=对角线积的一半的知识来判断.
解答:∵四边形ABCD为等腰梯形,∴∠A=∠B∵AD=BC,AB=AB,
∴△ADB≌△BCA,∴AC=DB,①正确;
∵CE⊥AB∴∠AEF=45°,由翻折得到EF⊥AC,∴∠CAB=45°由全等得到∠OBA=∠OAB=45°,∴∠OBA=∠AEF=45°那么EF∥BD,②对;
∠S四边形AECF=
 ×AC•EF,③错;
×AC•EF,③错;易得BE=(7-3)÷2=2,CE=AE=5,做FM⊥AB于点M,

∴CE:BE=FM:AM,∵FM=ME,∴AM=5-x,解得x=
 ,那么EF=
,那么EF= ④正确;
④正确;OG=OA-AG=
 -
-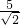 =
= ,FG=
,FG= -
- 易得OG≠FG,那么∠FOG≠45°,∴⑤错.
易得OG≠FG,那么∠FOG≠45°,∴⑤错.正确的序号是①②④.
点评:注意使用等腰梯形中的三角形全等,以及常用的辅助线方法,对角线互相垂直的四边形的面积=对角线积的一半等知识.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)
如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条) 如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.
如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF. 如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.
如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数. 如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.
如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.