题目内容
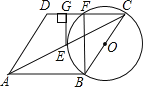
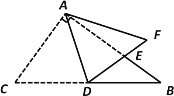
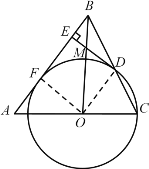
【题目】如图,在△ABC中,AB=AC=10,tan∠A=![]() ,点O是线段AC上一动点(不与点A,点C重合),以OC为半径的⊙O与线段BC的另一个交点为D,作DE⊥AB于E.
,点O是线段AC上一动点(不与点A,点C重合),以OC为半径的⊙O与线段BC的另一个交点为D,作DE⊥AB于E.
(1)求证:DE是⊙O的切线;
(2)当⊙O与AB相切于点F时,求⊙O的半径;
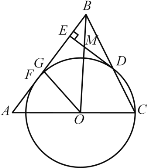
(3)在(2)的条件下,连接OB交DE于点M,点G在线段EF上,连接GO.若∠GOM=45°,求DM和FG的长.
【答案】(1)见解析;(2)r=![]() ;(3)DM=
;(3)DM=![]() ,FG=
,FG=![]()
【解析】
(1)连接OD,根据等腰三角形判断出∠ABC=∠ACB,进而得到OD∥AB即可得到求证;
(2)连接OF,根据切线得到△AOF是直角三角形,根据tan∠A=![]() ,设半径OF=OC=r,则可表示出AF=
,设半径OF=OC=r,则可表示出AF=![]() r,AO=10-r,勾股定理求出半径即可得到结果;
r,AO=10-r,勾股定理求出半径即可得到结果;
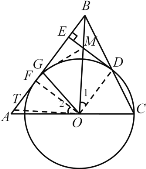
(3)现根据题意证出ODEF是正方形,求出BE,再根据△BEM∽△ODM,即可得到MD;在EF延长线上截取FT=DM,证明出OT=OM,再证明△OGT≌△OGM,则GM=GT=GF+FT=GF+DM,设出GF=a,根据勾股定理求解即可.
解:(1)证明:连接OD
∵OC,OD均为⊙O的半径,
∴OC=OD,
∴∠DCO=∠CDO
又∵在△ABC中,AB=AC,
∴∠ABC=∠ACB
∴∠ABC=∠CDO,
∴OD∥AB
∵DE⊥AB,
∴DE⊥OD
∴DE是⊙O的切线.
(2)解:连接OF,设⊙O的半径为r,则OF=r,OC=r
∵⊙O与AB相切于点F,
∴AB⊥OF,
∴∠OFA=90°,
在Rt△AOF中,∠OFA=90°,OF=r,tan∠A=![]()
∴AF=![]() r,
r,
∴AO=![]() r
r
又∵AO=AC-OC=10-r,
∴![]() r=10-r
r=10-r
∴ r=![]() .
.
(3)由(2)知r= ![]() ,
,
∴AF=![]() r=
r=![]()
∵∠ODE=∠DEF=∠OFE=90°,
∴四边形ODEF是矩形
∵OF=OD,
∴矩形ODEF是正方形,
∴DE=EF=OF= ![]()
∴BE=AB-AF-EF=10-![]() -
-![]() =
=![]()
∵∠BME=∠OMD,∠BEM=∠ODM=90°
∴△BEM∽△ODM,
∴![]()
即  =
= ![]() ,解得DM=
,解得DM=![]()
在EF延长线上截取FT=DM
∵四边形ODEF是正方形,
∴∠OFT=∠ODM=90°,OF=OD
∴△OFT≌△ODM,
∴∠2=∠1,OT=OM
∵∠DOF=90°,∠GOM=45°,
∴∠GOF+∠1=45°,
∴∠GOF+∠2=45°
即∠GOT=45°,
∴∠GOT=∠GOM
又OG=OG,
∴△OGT≌△OGM,
∴GM=GT=GF+FT=GF+DM
设GF=a,则EG= ![]() -a,GM=
-a,GM= ![]() +a,且EM=DE-DM=
+a,且EM=DE-DM=![]() -
-![]() =
= ![]()
在Rt△EMG中,EM 2+EG 2=GM 2,即(![]() )2+(
)2+(![]() -a )2=(
-a )2=(![]() +a )2,解得a=
+a )2,解得a=![]()
∴FG的长为![]() .
.