��Ŀ����
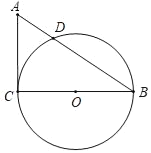
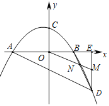
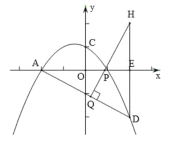
����Ŀ����ͼ�����κ���y��ax2+bx+1��ͼ��x����A����2��0����B��1��0�����㣬��y���ڵ�C����D�ǵ����������������ϵ�һ�����㣬����D��DE��y�ύx���ڵ�E���߶�CB���ӳ��߽�DE�ڵ�M������OM��BD���ڵ�N��
��1������κ����ı���ʽ��
��2����S��OEM��S��DBEʱ�����D�����꼰sin��DAE��ֵ��
��3���ڣ�2���������£���P��x����һ�����㣬��![]() ����Сֵ��
����Сֵ��
���𰸡���1��![]() ����2��
����2��![]() ��
��![]() ����3��
����3��![]()
��������
(1) �ô���ϵ��������![]() ��
��![]() ������������ʽ
������������ʽ![]() ���ɽ��
���ɽ��
(2)�������߿ɵ�BC�������꣬�����ô���ϵ�������ֱ��BC����ʽΪ![]() ����������D����Ϊ��
����������D������![]() ����
����![]() ��
��![]() ����
����![]() �ɵ�OE=DE����
�ɵ�OE=DE����![]() ���������D����Ϊ��2��-2�����������Ǻ�������
���������D����Ϊ��2��-2�����������Ǻ�������![]() �������.
�������.
(3)�ɺ�����ģ�Ϳ�֪������![]() ����
����![]() ת��ΪP�㵽AD�ľ���PQ������D����x��ĶԳƵ�
ת��ΪP�㵽AD�ľ���PQ������D����x��ĶԳƵ�![]() ����H��P��D���㹲����
����H��P��D���㹲����![]() ʱ��
ʱ��![]() ��СֵΪHQ��ֵ������
��СֵΪHQ��ֵ������![]() ���ɼ����
���ɼ����![]() .
.
��1������![]() ��
��![]() ������������ʽ
������������ʽ![]() �У�
�У�
��![]() ���
���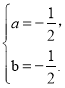
������κ����ı���ʽΪ![]() ��
��
��2����![]() ����
����![]() �ã�
�ã�![]() ����
����![]() ��
��
��ֱ��BC����ʽΪ![]() ������
������![]() ��
��![]() ������������ʽ�У�
������������ʽ�У�
��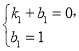 ���
���
��ֱ��BC�ı���ʽΪ![]() ��
��
��![]() ����
����![]() ��
��![]() ��
��
��![]() ��
��![]() ��BE=x-1��ME=x-1
��BE=x-1��ME=x-1
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() �����
�����![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
��![]() ����
����![]() ��
��
��3����ͼ������D����x��ĶԳƵ�![]() ������P��PQ��AD�ڵ�Q����
������P��PQ��AD�ڵ�Q����![]() ��
��
��![]() ��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��
��H��P��D���㹲����![]() ʱ��
ʱ��
![]() ��СֵΪHQ��ֵ��
��СֵΪHQ��ֵ��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��

 ��������ѧ����ϵ�д�
��������ѧ����ϵ�д� ��Ԫ������ĩ��ϵ�д�
��Ԫ������ĩ��ϵ�д�