题目内容
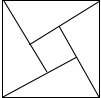如图是我国古代数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形、如果大正方形的面积13，小正方形的面积是1，直角三角形的短直角边为a，较长的直角边为b，那么（a+b）2的值为（ ）| A、169 | B、25 | C、19 | D、13 |
分析：先求出四个直角三角形的面积，再根据再根据直角三角形的边长求解即可．
解答：解：∵大正方形的面积13，小正方形的面积是1，
∴四个直角三角形的面积和是13-1=12，即4×
ab=12，
即2ab=12，a2+b2=13，
∴（a+b）2=13+12=25．
故选B．
∴四个直角三角形的面积和是13-1=12，即4×
| 1 |
| 2 |
即2ab=12，a2+b2=13，
∴（a+b）2=13+12=25．
故选B．
点评：注意完全平方公式的展开：（a+b）2=a2+b2+2ab，还要注意图形的面积和a，b之间的关系．
练习册系列答案
相关题目
（2012•六盘水）如图是我国古代数学家杨辉最早发现的，称为“杨辉三角”．它的发现比西方要早五百年左右，由此可见我国古代数学的成就是非常值得中华民族自豪的！“杨辉三角”中有许多规律，如它的每一行的数字正好对应了（a+b）n（n为非负整数）的展开式中a按次数从大到小排列的项的系数．例如，（a+b）2=a2+2ab+b2展开式中的系数1、2、1恰好对应图中第三行的数字；再如，（a+b）3=a3+3a2b+3ab2+b3展开式中的系数1、3、3、1恰好对应图中第四行的数字．请认真观察此图，写出（a+b）4的展开式，（a+b）4=
探究题
展开式中的系数1、2、1恰好对应图中第三行的数字；
展开式中的系数1、3、3、1恰好对应图中第四行的数字。
展开式中的系数1、2、1恰好对应图中第三行的数字；
展开式中的系数1、3、3、1恰好对应图中第四行的数字。