题目内容
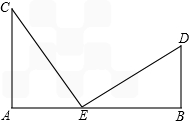
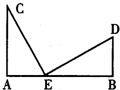23、如图，在东西走向的铁路上有A、B两站（视为直线上的两点）相距36千米，在A、B的正北分别有C、D两个蔬菜基地，其中C到A站的距离为24千米，D到B站的距离为l2千米，现要在铁路AB上建一个蔬菜加工厂E，使蔬菜基地C、D到E的距离相等，则E站应建在距A站12
千米的地方．分析：设AE=x千米，则BE=（36-x）千米，分别在Rt△AEC和Rt△BED中，利用勾股定理表示出CE和ED，然后通过CE=ED建立方程，解方程即可．
解答：解：设AE=x千米，则BE=（36-x）千米，
在Rt△AEC中，CE2=AE2+AC2=x2+242，
在Rt△BED中，DE2=BE2+BD2=（36-x）2+122，
∵CE=ED，
∴x2+242=（36-x）2+122，解得x=12，
所以E站应建在距A站12千米的地方，能使蔬菜基地C、D到E的距离相等．
故答案为12．
在Rt△AEC中，CE2=AE2+AC2=x2+242，
在Rt△BED中，DE2=BE2+BD2=（36-x）2+122，
∵CE=ED，
∴x2+242=（36-x）2+122，解得x=12，
所以E站应建在距A站12千米的地方，能使蔬菜基地C、D到E的距离相等．
故答案为12．
点评：本题考查了勾股定理的应用：利用勾股定理表示有关线段，然后建立等量关系，再解方程得到答案．
练习册系列答案
相关题目
如图，在东西走向的铁路上有A、B两站（视为直线上的两点）相距36千米，在A、B的正北分别有C、D两个蔬菜基地，其中C到A站的距离为24千米，D到B站的距离为12千米，现要在铁路AB上建一个蔬菜加工厂E，使蔬菜基地C、D到E的距离相等，则E站应建在距A站________千米的地方．