题目内容
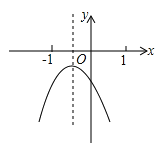
【题目】在直角坐标系xOy中,抛物线y=﹣![]() x2+
x2+![]() x+4与x轴交于A,B两点,与y轴交于点C连接AC,BC.
x+4与x轴交于A,B两点,与y轴交于点C连接AC,BC.
(1)求∠ACO的正弦值.
(2)如图1,D为第一象限内抛物线上一点,记点D横坐标为m,作DE∥AC交BC于点E,DH∥y轴交于BC于点H,请用含m的代数式表示线段DE的长,并求出当CH:BH=2:1时线段DE的长.
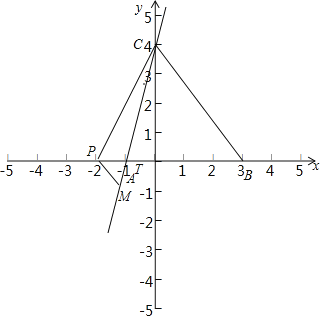
(3)如图2,P为x轴上一动点(P不与点A、B重合),作PM∥BC交直线AC于点M,连接CP,是否存在点P使S△CPM=2?若存在,请直接写出点P的坐标,若不存在,请说明理由.

【答案】(1)![]() .(2)
.(2)![]() .(3)P(1,0)、(2
.(3)P(1,0)、(2![]() +1,0)、(1﹣2
+1,0)、(1﹣2![]() ,0).
,0).
【解析】
试题分析:(1)利用抛物线解析式求出点A、C坐标,求出线段OA、AC长度,即可求出∠ACO的正弦值;
(2)首先设出点D坐标,写出点H坐标,利用相似三角形比例关系可求出线段DE的长,根据CH:BH=2:1,求出线段DE的长;
(3)设出点P坐标,写出直线PM解析式,表示出点M、及与y轴交点坐标,利用三角形面积求出点P坐标.
解(1)令x=0,y=4,
∴C(0,4),OC=4,
令y=0,x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0),OA=1,
∴AC=![]() =
=![]() ,
,
Sin∠ACO=![]() =
=![]() =
=![]() .
.
(2)如图1,
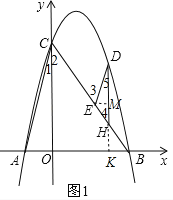
∵DE∥AC,
∴∠1+∠2=∠3=∠4+∠5,
∵DH∥y轴,
∴∠2=∠4,
∴∠1=∠5,
∴OA:OC=EM:DM,
过点E作EM⊥DH,垂足为M,
设点D(m,﹣![]() m2+
m2+![]() m+4),
m+4),
直线BC:y=﹣![]() x+4,
x+4,
∴H(m,﹣![]() m+4),
m+4),
∴DH=﹣![]() m2+4m,
m2+4m,
设EM=x,则DM=4x,
∠MEH=∠B,
∴HM=![]() x,DH=
x,DH=![]() x+4x=
x+4x=![]() x,
x,
∴x=![]() ,
,
∴DE=![]() x=
x=![]() =
=![]() (﹣
(﹣![]() m2+4m)=﹣
m2+4m)=﹣![]() m2+
m2+![]() m,
m,
当CH:BH=2:1时,
延长DH至点K,则OK:KB=2:1,
OK=2,
∴m=2.
∴DE=﹣![]() +
+![]() =
=![]() .
.
(3)P(1,0)、(2![]() +1,0)、(1﹣2
+1,0)、(1﹣2![]() ,0).
,0).
直线BC解析式为:y=﹣![]() x+4,
x+4,
直线AC解析式为:y=4x+4,
∵作PM∥BC交直线AC于点M,
∴设PM直线解析式为y=﹣![]() x+b,
x+b,
∴P(![]() ,0)
,0)
联立直线AC,求得M(![]() ,
,![]() ),
),
当点P在线段AB上时,如图:
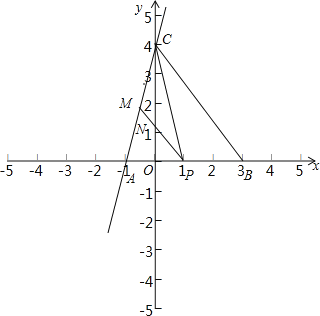
∴S△CPM=![]() ×CN×(
×CN×(![]() ﹣
﹣![]() )=2
)=2
∴![]() ×(4﹣b)×(
×(4﹣b)×(![]() ﹣
﹣![]() )=2
)=2
解得:b=![]() ,
,
∴P(1,0);
当点P在线段AB上,
连接CP,是否存在点P使S△CPM=2
当点P在线段AB延长线上时,如图:
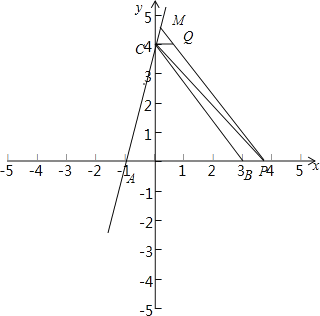
同理:P(![]() ,0),M(
,0),M(![]() ,
,![]() ),
),
做CQ⊥y轴,Q(![]() ,4)
,4)
∴S△CPM=![]() ×CQ×
×CQ×![]() =2
=2
解得:b=![]() ,
,
∴P(2![]() +1,0).
+1,0).
当点P在线段BA延长线上时,如图:
同理:P(![]() ,0),M(
,0),M(![]() ,
,![]() ),
),
∴S△CPM=![]() ×PA×(4﹣
×PA×(4﹣![]() )=2
)=2
解得:b=![]() ,
,
∴P(1﹣2![]() ,0).
,0).
综上所述:P(1,0)、(2![]() +1,0)、(1﹣2
+1,0)、(1﹣2![]() ,0).
,0).

 名校课堂系列答案
名校课堂系列答案