题目内容
(2002•烟台)如图,过点C的直线l∥x轴,抛物线y=ax2+bx+c(a<0)过A(-1,0),C(0,1)两点,且截直线l所得线段CD= .
.(1)求该抛物线的解析式;
(2)若点M(m,t)(m<0,t>0)在抛物线上,MN∥x轴,且与该抛物线的另一交点为N,问:是否存在实数t,使得MN=2AO?如果存在,求出t的值;如果不存在,请说明理由.
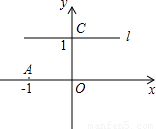
【答案】分析:(1)可根据A,C,D三点坐标用待定系数法来求出抛物线的解析式.本题中D点的坐标不确定,因此要分两种情况进行求解.
(2)由于抛物线的解析式有两个,因此要分类讨论.求解时,可设出N点的坐标,然后用M,N的横坐标表示出MN的长,根据韦达定理可用t表示出M、N两点横坐标的和与积,由此可用含t的式子表示出OA的长,即可求出t的值.
解答: 解:(1)∵l∥x轴,C(0,1),CD=
解:(1)∵l∥x轴,C(0,1),CD= ,
,
∴D点坐标为D(- ,1)或D(
,1)或D( ,1),
,1),
当抛物线过A(-1,0),C(0,1),D(- ,1)时.
,1)时.
 ,
,
解得 ,
,
当抛物线过A(-1,0),C(0,1),D( ,1)时.
,1)时.
 ,
,
解得 ,
,
故所求的抛物线的解析式为y=-3x2-2x+1或y=- x2+
x2+ x+1.
x+1.
(2)若点M(m,t)在抛物线y=-3x2-2x+1上,
因抛物线对称轴在y轴左侧,线段MN在x轴上方,
故MN<2AO.
因此不存在实数t,使得MN=2AO.
若点M(m,t)在抛物线y=- x2+
x2+ x+1上,
x+1上,
则存在实数t,使得MN=2AO.
设N(n,t),
则有t=- n2+
n2+ n+1,又t=-
n+1,又t=- m2+
m2+ m+1.
m+1.
故m、n是方程- x2+
x2+ x+1-t=0的两个实数根.
x+1-t=0的两个实数根.
∴m+n= ,mn=-
,mn=- (1-t),
(1-t),
∴MN=n-m= =
= =2AO=2,
=2AO=2,
∴t= .
.
点评:数形结合、方程函数的数学思想在数学综合题中充分利用,对题目的条件和结论既分析其代数含义又分析其几何意义,力图在代数和几何的结合上找出解题思路.
(2)由于抛物线的解析式有两个,因此要分类讨论.求解时,可设出N点的坐标,然后用M,N的横坐标表示出MN的长,根据韦达定理可用t表示出M、N两点横坐标的和与积,由此可用含t的式子表示出OA的长,即可求出t的值.
解答:
 解:(1)∵l∥x轴,C(0,1),CD=
解:(1)∵l∥x轴,C(0,1),CD= ,
,∴D点坐标为D(-
 ,1)或D(
,1)或D( ,1),
,1),当抛物线过A(-1,0),C(0,1),D(-
 ,1)时.
,1)时. ,
,解得
 ,
,当抛物线过A(-1,0),C(0,1),D(
 ,1)时.
,1)时. ,
,解得
 ,
,故所求的抛物线的解析式为y=-3x2-2x+1或y=-
 x2+
x2+ x+1.
x+1.(2)若点M(m,t)在抛物线y=-3x2-2x+1上,
因抛物线对称轴在y轴左侧,线段MN在x轴上方,
故MN<2AO.
因此不存在实数t,使得MN=2AO.
若点M(m,t)在抛物线y=-
 x2+
x2+ x+1上,
x+1上,则存在实数t,使得MN=2AO.
设N(n,t),
则有t=-
 n2+
n2+ n+1,又t=-
n+1,又t=- m2+
m2+ m+1.
m+1.故m、n是方程-
 x2+
x2+ x+1-t=0的两个实数根.
x+1-t=0的两个实数根.∴m+n=
 ,mn=-
,mn=- (1-t),
(1-t),∴MN=n-m=
 =
= =2AO=2,
=2AO=2,∴t=
 .
.点评:数形结合、方程函数的数学思想在数学综合题中充分利用,对题目的条件和结论既分析其代数含义又分析其几何意义,力图在代数和几何的结合上找出解题思路.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
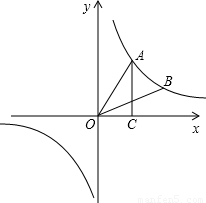
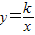 的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴,垂足为点C,且△AOC的面积为2.
的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴,垂足为点C,且△AOC的面积为2.
 .
.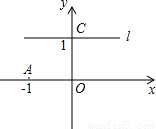
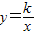 的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴,垂足为点C,且△AOC的面积为2.
的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴,垂足为点C,且△AOC的面积为2.