题目内容
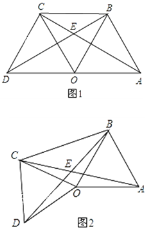
【题目】如图1,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC.
(1)证明:⊿ABC ≌ ⊿DCB;
(2)求∠AEB的大小.
(3)如图2,△OAB固定不动,保持△OCD的形状和大小不变,将△OCD绕点O旋转(△OAB和△OCD不能重叠),求∠AEB的大小.
【答案】(1)详见解析;(2)60° (3)60°
【解析】
(1)利用题中信息可得:![]() 都为等边三角形,找出它们之间的等量关系去证明全等;
都为等边三角形,找出它们之间的等量关系去证明全等;
(2)根据等边三角形和外角的性质,可求![]() ;
;
(3)方法同上,只是![]() ,此时已不是外角,但仍可用外角和内角的关系解答.
,此时已不是外角,但仍可用外角和内角的关系解答.
证明:(1)
![]() ,且
,且![]() 都为等边三角形,
都为等边三角形,
![]() ,
,
![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
![]() ;
;
(2)如图所示:

![]() 和
和![]() 都是等边三角形,
都是等边三角形,
且点O是线段![]() 的中点,
的中点,
![]() ,∠
,∠![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
同理![]() ,
,
![]()
![]() .
.
(3)如图所示:

![]() 都是等边三角形,
都是等边三角形,
![]()
又![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,![]() ,
,
![]()
![]()

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目