题目内容
在Rt△ABC中，∠ACB=90°，∠B=30°，AC=
cm，则AB边上的中线为
- A.1cm
- B.2cm
- C.1.5cm
- D.cm
D
分析：由直角三角形的性质知：斜边上的中线等于斜边的一半；已知了直角三角形的两条直角边，由勾股定理可求得斜边的长，由此得解
解答：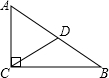
解：∵Rt△ABC中，AC=cm，且∠ACB=90°，∠B=30°，
∴AB=2，
∴AB边上的中线CD=
AB=cm．
故选D．
点评：此题主要考查直角三角形斜边上的中线等于斜边的一半等知识点的理解和掌握，难度不大，属于基础题．
分析：由直角三角形的性质知：斜边上的中线等于斜边的一半；已知了直角三角形的两条直角边，由勾股定理可求得斜边的长，由此得解
解答：
解：∵Rt△ABC中，AC=cm，且∠ACB=90°，∠B=30°，∴AB=2
，∴AB边上的中线CD=
AB=cm．故选D．
点评：此题主要考查直角三角形斜边上的中线等于斜边的一半等知识点的理解和掌握，难度不大，属于基础题．
练习册系列答案
相关题目
已知：如图，在Rt△ABC中，∠C=90°，AC=12，BC=9，D是AB上一点，以BD为直径的⊙O切AC于E，求⊙O的半径．
如图，已知：在Rt△ABC中，∠C=90°，AB=12，点D是AB的中点，点O是△ABC的重心，则OD的长为（ ）在Rt△ABC中，已知a及∠A，则斜边应为（ ）
| A、asinA | ||
B、
| ||
| C、acosA | ||
D、
|
如图，在Rt△ABC中，∠C=90°，CD⊥AB于D，且AD：BD=9：4，则AC：BC的值为（ ）| A、9：4 | B、9：2 | C、3：4 | D、3：2 |