Question

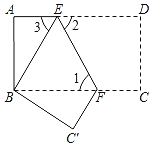
【题目】如图，将矩形纸片放入以所在直线为轴，边上一点为坐标原点的平面直角坐标系中，连结。将纸片沿折叠，点恰好落在边上点处，若，则点的坐标为________________。

Answer 1

【答案】（，1）

【解析】

依据折叠的性质以及勾股定理，即可得出AC'的长，进而得到BC'=1，再根据勾股定理可得，Rt△BOC'中，BO2+BC'2=C'O2，列方程求解即可得到BO=，进而得出点C的坐标．

解：∵矩形纸片ABCD中，AB=5，BC=3，且纸片沿折叠，点恰好落在边上点处，

∴AD=3，CD=C'D=5，

∴Rt△ADC'中，AC'=

∴BC'=5-4=1，

设BO=x，则CO=C'O=3-x，

∵Rt△BOC'中，BO2+BC'2=C'O2，

∴x2+12=（3-x）2，

解得x=，

∴点的坐标为（，1），

故答案为：（，1），