题目内容

如图，已知△ABC的面积S△ABC=1．

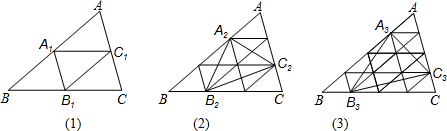
在图（1）中，若
AA1
AB
=
BB1
BC
=
CC1
CA
=
1
2
，则S △A1B1C1=
1
4
；
在图（2）中，若
AA2
AB
=
BB2
BC
=
CC2
CA
=
1
3
，则S △A2B2C2=
1
3
；
在图（3）中，若
AA3
AB
=
BB3
BC
=
CC3
CA
=
1
4
，则S △A3B3C3=
7
16
；
按此规律，若
AA4
AB
=
BB4
BC
=
CC4
CA
=
1
5
，则S △A4B4C4=
13
25
13
25
；
若
AA8
AB
=
BB8
BC
=
CC8
CA
=
1
9
，则S △A8B8C8=
57
81
57
81
．
分析：观察三个图形下得出三角形的面积，归纳总结得到一般性规律，即可求出第四个与第八个图形的面积．
解答：解：若
AA1
AB
=
BB1
BC
=
CC1
CA
=
1
2
，则S△A1B1C1=1-3×
1
2
×
1
2
=
1
4
；
若
AA2
AB
=
BB2
BC
=
CC2
CA
=
1
3
，则S△A2B2C2=1-3×
2
3
×
1
3
=
1
3
；
若
AA3
AB
=
BB3
BC
=
CC3
CA
=
1
4
，则S△A3B3C3=1-3×
3
4
×
1
4
=
7
16
；
若
AA4
AB
=
BB4
BC
=
CC4
CA
=
1
5
，则S△A4B4C4=1-3×
4
5
×
1
5
=
13
25
；
若
AA8
AB
=
BB8
BC
=
CC8
CA
=
1
9
，则S△A8B8C8=1-3×
8
9
×
1
9
=
57
81
．
故答案为：
13
25
；
57
81
点评：此题考查了相似三角形的判定与性质，弄清题中的规律是解本题的关键．
练习册系列答案
相关题目
如图，已知△ABC的面积S△ABC=1．
在图1中，若
AA1
AB
=
BB1
BC
=
CC1
CA
=
1
2
，则S△A1B1C1=
1
4
；
在图2中，若
AA2
AB
=
BB2
BC
=
CC2
CA
=
1
3
，则S△A2B2C2=
1
3
；
在图3中，若
AA3
AB
=
BB3
BC
=
CC3
CA
=
1
4
，则S△A3B3C3=
7
16
；
按此规律，若
AA8
AB
=
BB8
BC
=
CC8
CA
=
1
9
，S△A8B8C8=
 
．
精英家教网
精英家教网如图，已知△ABC的面积为4，且AB=AC，现将△ABC沿CA方向平移CA的长度，得到△EFA．
（1）判断AF与BE的位置关系，并说明理由；
（2）若∠BEC=15°，求AC的长．
（2012•温州二模）如图，已知△ABC的面积是2平方厘米，△BCD的面积是3平方厘米，△CDE的面积是3平方厘米，△DEF的面积是4平方厘米，△EFG的面积是3平方厘米，△FGH的面积是5平方厘米，那么，△EFH的面积是
4
4
 平方厘米．
（2010•孝感模拟）如图，已知△ABC的三个顶点的坐标分别为A（-2，2）、B（-5，0）、C（-1，0）．
（1）请直接写出点A关于y轴对称的点的坐标；
（2）将△ABC绕坐标原点O逆时针旋转90°得到△A1B1C1，再将△A1B1C1以C1为位似中心，放大2倍得到△A2B2C1，请画出△A1B1C1和△A2B2C1，并写出一个点A2的坐标．（只画一个△A2B2C1即可）
如图，已知△ABC的三个顶点的坐标分别是A（-7，1），B（-3，3），C（-2，6）．
（1）求作一个三角形，使它与△ABC关于y轴对称；
（2）写出（1）中所作的三角形的三个顶点的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网