题目内容
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() ,如果点
,如果点![]() 的纵坐标满纵坐标满足:
的纵坐标满纵坐标满足: 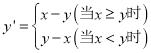 ,那么称点
,那么称点![]() 为点
为点![]() 的“关联点”.
的“关联点”.
(1)请直接写出点![]() 的“关联点”的坐标____________;
的“关联点”的坐标____________;
(2)若点![]() 在函数
在函数![]() 的图像上,其“关联点”
的图像上,其“关联点”![]() 与点
与点![]() 重合,求点
重合,求点![]() 的坐标;
的坐标;
(3)若点![]() 的“关联点”
的“关联点”![]() 在函数
在函数![]() 的图像上,当
的图像上,当![]() 时,求线段
时,求线段![]() 的最大值.
的最大值.
【答案】(1)(3,2);(2)(4,2);(3)当m≥n时,MN有最大值为14;当m<n时,线段MN的最大值为2.
【解析】
(1)根据关联点的定义,即可得到答案;
(2)根据关联点的定义,可得到Q点坐标,根据点重合,得到方程,解方程即可得到答案;
(3)根据关联点的定义,分成两种情况,当m≥n时,与当m<n时,在每种情况下,求出N的坐标,根据平行于y的直线上的两点的距离,可得到二次函数,然后根据二次函数性质求函数的最大值即可.
(1)∵3<5,根据关联点定义
∴y’=5-3=2
故点(3,5)的“关联点”的坐标为(3,2).
(2)P在函数y=x-2的图像上
设P点坐标为(x,x-2)
∵x>x-2,根据关联点定义得到Q点(x,2)
又因为P、Q重合,所以有2=x-2,得到x=4
∴P点坐标为(4,2).
(3)点![]() 的“关联点”是
的“关联点”是![]() ,共分两种情况考虑.
,共分两种情况考虑.
①当m≥n时,点N的坐标为(m,m-n)
∵N在二次函数![]() 上
上
∴m-n=2m2,得到n=-2m2+m,
∴yM =-2m2+m,yN=2m2
∴MN=丨yM- yN丨=丨-4m2+m丨
当0≤m≤![]() ,-4m2+m≥0,
,-4m2+m≥0,
MN=-4m2+m=-4(m-![]() )2+
)2+![]()
∴当m=![]() 时,线段MN的最大值为
时,线段MN的最大值为![]() .
.
当![]() <m≤2时,-4m2+m<0,
<m≤2时,-4m2+m<0,
∴MN=4m2-m=4(m-![]() )2-
)2-![]() ,当m=2时,MN有最大值为14
,当m=2时,MN有最大值为14
∴当m≥n时,MN有最大值为14;
②当m<n时,点N的坐标为(m,n-m)
∵N在二次函数![]() 上
上
∴n-m=2m2,即n=2m2+m
∴yM =2m2+m,yN=2m2
∴MN=丨yM- yN丨=丨m丨
∵![]()
∴MN=m
当m=2时,线段MN的最大值为2.
即当m<n时,线段MN的最大值为2.
∴综上,当m≥n时,MN有最大值为14;当m<n时,线段MN的最大值为2.

 阅读快车系列答案
阅读快车系列答案【题目】一个二次函数图像上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
| … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| … |
| 0 |
| 2 |
| 0 |
| -6 |
| … |
(1)![]() 的值为______;
的值为______;
(2)在给定的直角坐标系中,画出这个函数的图像;
(3)当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【题目】函数图象在探索函数的性质中有非常重要的作用,下面我们就一类特殊的函数展开探索.画函数![]() 的图象,经历分析解析式、列表、描点、连线过程得到函数图象如图所示;经历同样的过程画函数
的图象,经历分析解析式、列表、描点、连线过程得到函数图象如图所示;经历同样的过程画函数![]() 和
和![]() 的图象如图所示.
的图象如图所示.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣6 | ﹣4 | ﹣2 | 0 | ﹣2 | ﹣4 | ﹣6 | … |
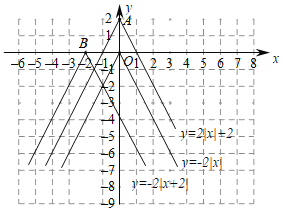
(1)观察发现:三个函数的图象都是由两条射线组成的轴对称图形;三个函数解折式中绝对值前面的系数相同,则图象的开口方向和形状完全相同,只有最高点和对称轴发生了变化.写出点A,B的坐标和函数![]() 的对称轴.
的对称轴.
(2)探索思考:平移函数![]() 的图象可以得到函数
的图象可以得到函数![]() 和
和![]() 的图象,分别写出平移的方向和距离.
的图象,分别写出平移的方向和距离.
(3)拓展应用:在所给的平面直角坐标系内画出函数![]() 的图象.若点
的图象.若点![]() 和
和![]() 在该函数图象上,且
在该函数图象上,且![]() ,比较
,比较![]() ,
,![]() 的大小.
的大小.