题目内容
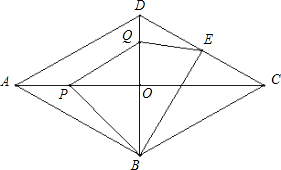 如图,在菱形ABCD中,AB=2cm,∠BAD=60°,E为CD边中点,点P从点A开始沿AC方向以每秒2
如图,在菱形ABCD中,AB=2cm,∠BAD=60°,E为CD边中点,点P从点A开始沿AC方向以每秒2| 3 |
(1)当点P在线段AO上运动时.
①请用含x的代数式表示OP的长度;
②若记四边形PBEQ的面积为y,求y关于x的函数关系式(不要求写出自变量的取值范围);
(2)显然,当x=0时,四边形PBEQ即梯形ABED,请问,当P在线段AC的其他位置时,以P,B,E,Q为顶点的四边形能否成为梯形?若能,求出所有满足条件的x的值;若不能,请说明理由.
分析:(1)①根据菱形的性质求出OA的长度,再求出AP的长等于2
x,OP的长即可求出;
②过E作EH⊥BD于H,表示出BQ的长等于2-x,分别求出△BPQ和△BEQ的面积,两个三角形的面积之和就是四边形PBEQ的面积为y.(2)根据梯形的定义,可以分三种情况讨论:
①PQ∥BE时,因为∠EBQ=30°,所以∠PQO=30°,再利用∠PQO的正切值列出算式即可求解,
②PE∥BQ时,因为点E是CD的中点,所以点P是CO的中点,根据AP的长度等于速度乘以时间列出算式即可求出;
③EQ∥BP时,过E作EH⊥DO,垂足为H,得到△QEH与△BPO相似,再根据相似三角形对应边成比例列出等式即可求出x的值.
| 3 |
②过E作EH⊥BD于H,表示出BQ的长等于2-x,分别求出△BPQ和△BEQ的面积,两个三角形的面积之和就是四边形PBEQ的面积为y.(2)根据梯形的定义,可以分三种情况讨论:
①PQ∥BE时,因为∠EBQ=30°,所以∠PQO=30°,再利用∠PQO的正切值列出算式即可求解,
②PE∥BQ时,因为点E是CD的中点,所以点P是CO的中点,根据AP的长度等于速度乘以时间列出算式即可求出;
③EQ∥BP时,过E作EH⊥DO,垂足为H,得到△QEH与△BPO相似,再根据相似三角形对应边成比例列出等式即可求出x的值.
解答: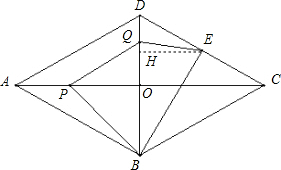 解:(1)①由题意得∠BAO=30°,AC⊥BD,
解:(1)①由题意得∠BAO=30°,AC⊥BD,
∵AB=2,
∴OB=OD=1,OA=OC=
,
∴OP=
-2
x,(2分)
②过点E作EH⊥BD,则EH为△COD的中位线,
∴EH=
OC=
,
∵DQ=x,
∴BQ=2-x,
∴y=S△BPQ+S△BEQ=
×(2-x)(
-2
x)+
×(2-x)×
,
=
x2-
x+
;(3分)
(2)能成为梯形,分三种情况:
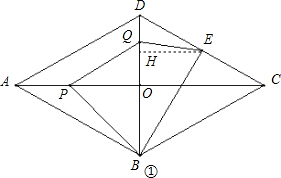
①当PQ∥BE时,∠PQO=∠DBE=30°,
∴
=tan30o=
,
即
=
,
∴x=
,
此时PB不平行QE,
∴x=
时,四边形PBEQ为梯形.(2分)
②当PE∥BQ时,P为OC中点,
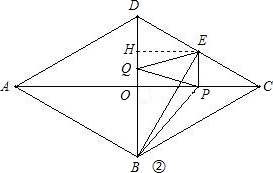
∴AP=
,即2
x=
,
∴x=
,
此时,BQ=2-x=
≠PE,
∴x=
时,四边形PEQB为梯形.(2分)
③
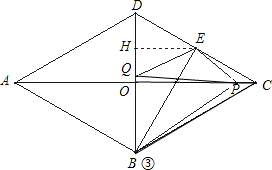
当EQ∥BP时,过E作EH⊥DO,垂足为H,
∴△QEH∽△BPO,
∴
=
,
∴
=
,
∴x=1(x=0舍去),
此时,BQ不平行于PE,
∴x=1时,四边形PEQB为梯形.(2分)
综上所述,当x=
、
或1时,以P,B,E,Q为顶点的四边形是梯形.
 解:(1)①由题意得∠BAO=30°,AC⊥BD,
解:(1)①由题意得∠BAO=30°,AC⊥BD,∵AB=2,
∴OB=OD=1,OA=OC=
| 3 |
∴OP=
| 3 |
| 3 |
②过点E作EH⊥BD,则EH为△COD的中位线,
∴EH=
| 1 |
| 2 |
| ||
| 2 |
∵DQ=x,
∴BQ=2-x,
∴y=S△BPQ+S△BEQ=
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
=
| 3 |
11
| ||
| 4 |
3
| ||
| 2 |
(2)能成为梯形,分三种情况:

①当PQ∥BE时,∠PQO=∠DBE=30°,
∴
| OP |
| OQ |
| ||
| 3 |
即
| ||||
| 1-x |
| ||
| 3 |
∴x=
| 2 |
| 5 |
此时PB不平行QE,
∴x=
| 2 |
| 5 |
②当PE∥BQ时,P为OC中点,

∴AP=
3
| ||
| 2 |
| 3 |
3
| ||
| 2 |
∴x=
| 3 |
| 4 |
此时,BQ=2-x=
| 5 |
| 4 |
∴x=
| 3 |
| 4 |
③

当EQ∥BP时,过E作EH⊥DO,垂足为H,
∴△QEH∽△BPO,
∴
| HE |
| OP |
| QH |
| BO |
∴
| ||||
2
|
x-
| ||
| 1 |
∴x=1(x=0舍去),
此时,BQ不平行于PE,
∴x=1时,四边形PEQB为梯形.(2分)
综上所述,当x=
| 2 |
| 5 |
| 3 |
| 4 |
点评:本题考查菱形的性质及梯形的判定方法,熟练掌握性质和定义是解本题的关键.本题还要注意说明以P,B,E,Q为顶点的四边形是梯形时,因为底边不确定,所以一定要分情况讨论.

练习册系列答案
相关题目
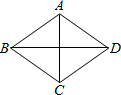 如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )
如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )| A、5 | B、10 | C、6 | D、8 |
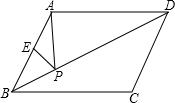
 ME交射线CD于点N,连接MD、AN.
ME交射线CD于点N,连接MD、AN. (2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA=
(2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA= 如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.
如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.