题目内容
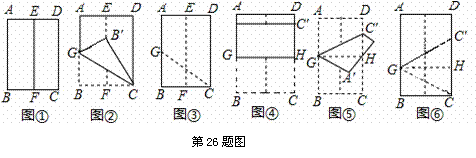
如图所示,将矩形纸片ABC![]() D按如下顺序进行折叠:对折,展平,得折痕EF(如图①);沿CG折叠,使点B落在EF上的点B′处,(如图②);展平,得折痕GC(如图③);沿GH折叠,使点C落在DH上的点C′处,(如图④);沿GC′折叠(如图
D按如下顺序进行折叠:对折,展平,得折痕EF(如图①);沿CG折叠,使点B落在EF上的点B′处,(如图②);展平,得折痕GC(如图③);沿GH折叠,使点C落在DH上的点C′处,(如图④);沿GC′折叠(如图
⑤);展平,得折痕GC′,GH(如图 ⑥).
(1)求图 ②中∠BCB′的大小.
(2)图⑥中的△GCC![]() ′是正三角形吗?请说明理由.
′是正三角形吗?请说明理由.
![]()
分析:(1)由折叠的性质知:=BC,然后在Rt△中,求得cos∠的值,利用特殊角的三角函数值的知识即可求得∠BCB′的度数;
(2)首先根据题意得:GC平分∠BCB′,即可求得∠GCC′的度数,然后由折叠的性质知:GH是线段CC′的对称轴,可得GC′=GC,即可得△GCC′是正三角形.
解:(1)由折叠的性质知: =BC,
在Rt△中,∵ cos∠=,∴ ∠=60°,即∠BCB′=60°.
(2)根据题意得:GC平分∠BCB′,∴ ∠GCB=∠GCB′=∠BCB′=30°,
∴ ∠GCC′=∠BCD-∠BCG=60°.
由折叠的性质知:GH是线段CC′的对称轴,∴ GC′=GC,∴ △GCC′是正三角形.

练习册系列答案
相关题目



 8、如图所示,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠EFC′=125°,那么∠ABE的度数为( )
8、如图所示,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠EFC′=125°,那么∠ABE的度数为( )