题目内容
已知 ,
, 且x≠y,求
且x≠y,求 的值.
的值.
解:∵ ,
, ,
,
∴x2+ y=y2+
y=y2+ x,
x,
∴x2-y2= x-
x- y,
y,
∴(x-y)(x+y- )=0,
)=0,
∵x≠y,
∴x+y= .
.
又∵x2+y2=( -
- y)+(
y)+( -
- x)=2
x)=2 -2,
-2,
∴x2+y2+2xy=(x+y)2=2,
即2 -2+2xy=2,
-2+2xy=2,
∴xy=2- .
.
∴ =
=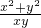 =
= =
=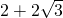 .
.
分析:由于 =
=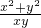 ,故只需分别求出x2+y2与xy的值即可.而由已知等式易知x2+y2=2
,故只需分别求出x2+y2与xy的值即可.而由已知等式易知x2+y2=2 +
+ (x+y),故先求出x+y的值,再代入计算出x2+y2的值,然后结合完全平方公式得出xy的值.通过观察发现,两个等式的右边都是
(x+y),故先求出x+y的值,再代入计算出x2+y2的值,然后结合完全平方公式得出xy的值.通过观察发现,两个等式的右边都是 ,所以左边相等,得到x2+
,所以左边相等,得到x2+ y=y2+
y=y2+ x,将它变形,可得x+y=
x,将它变形,可得x+y= ①;进一步计算出x2+y2=2
①;进一步计算出x2+y2=2 -2②,把①式两边平方,再将②式代入,可得xy=2-
-2②,把①式两边平方,再将②式代入,可得xy=2- ③,然后将所求式子通分,把②③代入,即可求出其值.
③,然后将所求式子通分,把②③代入,即可求出其值.
点评:本题主要考查了完全平方公式及代数式求值,难度中等,关键是求出x+y的值.
 ,
, ,
,∴x2+
 y=y2+
y=y2+ x,
x,∴x2-y2=
 x-
x- y,
y,∴(x-y)(x+y-
 )=0,
)=0,∵x≠y,
∴x+y=
 .
.又∵x2+y2=(
 -
- y)+(
y)+( -
- x)=2
x)=2 -2,
-2,∴x2+y2+2xy=(x+y)2=2,
即2
 -2+2xy=2,
-2+2xy=2,∴xy=2-
 .
.∴
 =
=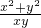 =
= =
=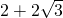 .
.分析:由于
 =
=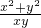 ,故只需分别求出x2+y2与xy的值即可.而由已知等式易知x2+y2=2
,故只需分别求出x2+y2与xy的值即可.而由已知等式易知x2+y2=2 +
+ (x+y),故先求出x+y的值,再代入计算出x2+y2的值,然后结合完全平方公式得出xy的值.通过观察发现,两个等式的右边都是
(x+y),故先求出x+y的值,再代入计算出x2+y2的值,然后结合完全平方公式得出xy的值.通过观察发现,两个等式的右边都是 ,所以左边相等,得到x2+
,所以左边相等,得到x2+ y=y2+
y=y2+ x,将它变形,可得x+y=
x,将它变形,可得x+y= ①;进一步计算出x2+y2=2
①;进一步计算出x2+y2=2 -2②,把①式两边平方,再将②式代入,可得xy=2-
-2②,把①式两边平方,再将②式代入,可得xy=2- ③,然后将所求式子通分,把②③代入,即可求出其值.
③,然后将所求式子通分,把②③代入,即可求出其值.点评:本题主要考查了完全平方公式及代数式求值,难度中等,关键是求出x+y的值.

练习册系列答案
相关题目
 ∥
∥ ,且
,且 ,
, ,
, ,求
,求 的长.
的长.
 是Rt
是Rt ABC的外接圆,
ABC的外接圆, ABC=90
ABC=90 ,点P是
,点P是
 ,BC=2,求
,BC=2,求 ∥
∥ ,且
,且 ,
, ,
, ,求
,求 的长.
的长.