��Ŀ����
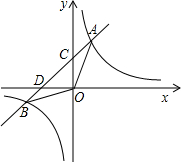
��֪��ͼ��һ�κ�����ͼ����һ�����������ޣ����뷴����������ͼ����A��B���㣬��y�ύ�ڵ�C��OB= ��tan��DOB=
��tan��DOB=
��1�����������Ľ���ʽ��
��2�����A�ĺ�����Ϊm����ABO�����ΪS����S��m�ĺ�����ϵʽ����д���Ա���m��ȡֵ��Χ��
��3������OCD��������� �����жϹ�A��B�������������x���Ͻصõ��߶γ��ܷ��
�����жϹ�A��B�������������x���Ͻصõ��߶γ��ܷ�� ��3������ܣ����ʱ�����ߵĽ���ʽ��������ܣ���˵�����ɣ�
��3������ܣ����ʱ�����ߵĽ���ʽ��������ܣ���˵�����ɣ�
 �⣺��1������A��AG��x���ڵ�G������B��BH��x���ڵ�H����Rt��OHB�У�
�⣺��1������A��AG��x���ڵ�G������B��BH��x���ڵ�H����Rt��OHB�У���tan��HOB=
 =
= ��
����HO=3BH��
�ɹ��ɶ����ã�BH2+HO2=OB2��
�֡�OB=
 ��
����BH2+��3BH��2=��
 ��2��
��2����BH��0��
��BH=1��HO=3��
���B��-3��-1����
�跴���������Ľ���ʽΪy=
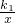 ��k1��0����
��k1��0�����ߵ�B�ڷ�����������ͼ���ϣ���k1=3��
�෴���������Ľ���ʽΪy=
 ��
����2����ֱ��AB�Ľ���ʽΪy=k2x+b��k2��0�����ɵ�A�ڵ�һ���ޣ���m��0��
���е�A�ں���y=
 ��ͼ���ϣ�����õ�A��������Ϊ��m��
��ͼ���ϣ�����õ�A��������Ϊ��m�� ����
������Ϊtan��DOB=
 ��OB=
��OB= ��
����BH=a����HO=3a��
���Ǹ��ݹ��ɶ�����a2+9a2=10��
���a=��1��
��B��������-3��-1����
��A��B��������ֱ�������ʽ�ã�
 ��
�����k=
 ��b=
��b= ��
����������ʽΪy=
 x+
x+ ��
����C��0��
 ����
��������S=
 ��m+3����
��m+3���� =
= ��
������0��m��3��
��3��A��B�������������x���Ͻصõ��߶γ��ܵ���3��
���B��-3��-1����A��1��3���������߽���ʽΪy=ax2+bx+c��

�ɵ�
 ��
�����b=2a+1��c=2-3a��
����ΪA��B�������������x���Ͻصõ��߶γ�����3��
������A��x1��0������x2��0����x2��x1��
�ɵ�x2-x1=3������ƽ���ã�x2+x1��2-4x1x2=9��
���ݸ���ϵ���Ĺ�ϵ��-
 ��2-4•
��2-4• =9����c=2-3a��b=2a+1���룬
=9����c=2-3a��b=2a+1���룬��16a2-13a+1=0��
a=
 ��
����a=
 ʱ��b=2a+1=
ʱ��b=2a+1= ��c=
��c= ��
����a=
 ʱ��b=
ʱ��b= ��c=
��c=
��A��B�������������x���Ͻصõ��߶γ��ܵ���3��
�����Ľ���ʽ��y=
 x2+
x2+ x+
x+ ��y=
��y= x2+
x2+ x+
x+ ��
����������1������tan��DOB=
 ��֪Rt��OHB����ֱ�DZߵıȣ�����ΪOB=10�����Կɸ��ݹ��ɶ��������B�����꣬�����������ʽ��
��֪Rt��OHB����ֱ�DZߵıȣ�����ΪOB=10�����Կɸ��ݹ��ɶ��������B�����꣬�����������ʽ����2����֪A�������m�����뷴������������ʽ�������A�����꣬����OB=
 ��tan��DOB=
��tan��DOB= �������ù��ɶ������B�����ꣻ
�������ù��ɶ������B�����ꣻ��A��B��������ֱ����һ�κ���y=k2x+b�Ľ���ʽ���ⷽ����õ�k2��b��ֵ����m��ʾ����Ȼ�����һ�κ��������ʣ����C�����꣬���ó�OC�ij����������OCΪ�ױߣ���A��B���������ľ���ֵΪ�ߵ����������Ρ�OCA�͡�COB�����֮�ͣ�
��3����������߽���ʽ����B��-3��-1����A��1��3���ֱ�������ʽ�����b��ֵ�Լ�a��c�Ĺ�ϵʽ���ٸ��ݸ���ϵ���Ĺ�ϵ���
���������⽫һ�κ��������κ�������������������������к�ǿ���ۺ��ԣ�����ͼ�������������Ӧ�߶εij���ת��ΪһԪ���η��̸���ϵ���Ĺ�ϵ���

��ϰ��ϵ�д�
 Сѧ��ѧ������ѿڶ���ϵ�д�
Сѧ��ѧ������ѿڶ���ϵ�д� ������Ӧ�������������ϵ�д�
������Ӧ�������������ϵ�д� �㽭֮�ǿ�ʱ�Ż���ҵϵ�д�
�㽭֮�ǿ�ʱ�Ż���ҵϵ�д�
�����Ŀ
 ��3������ܣ����ʱ�����ߵĽ���ʽ��������ܣ���˵�����ɣ�
��3������ܣ����ʱ�����ߵĽ���ʽ��������ܣ���˵�����ɣ�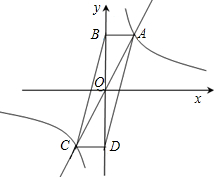 ��֪��ͼ��һ�κ���y=2x�뷴��������
��֪��ͼ��һ�κ���y=2x�뷴�������� ��tan��DOB=
��tan��DOB=
 �����жϹ�A��B�������������x���Ͻصõ��߶γ��ܷ����3������ܣ����ʱ�����ߵĽ���ʽ��������ܣ���˵�����ɣ�
�����жϹ�A��B�������������x���Ͻصõ��߶γ��ܷ����3������ܣ����ʱ�����ߵĽ���ʽ��������ܣ���˵�����ɣ�
 ��tan��DOB=
��tan��DOB=
 �����жϹ�A��B�������������x���Ͻصõ��߶γ��ܷ����3������ܣ����ʱ�����ߵĽ���ʽ��������ܣ���˵�����ɣ�
�����жϹ�A��B�������������x���Ͻصõ��߶γ��ܷ����3������ܣ����ʱ�����ߵĽ���ʽ��������ܣ���˵�����ɣ�