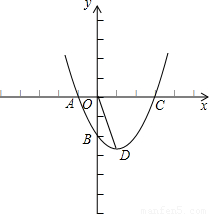题目内容
(2004•本溪)已知,如图,抛物线y=ax2+bx+c经过点A(-1,0),B(0,-3),C(3,0 )三点.(1)求抛物线的解析式;
(2)若抛物线的顶点为D,求sin∠BOD的值.
【答案】分析:(1)把点A(-1,0),B(0,-3),C(3,0 )三点的坐标代入函数解析式,利用待定系数法求解;
(2)求出抛物线的顶点坐标,根据正弦函数的定义求解.
解答: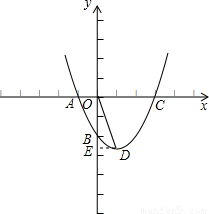 解:(1)由已知得
解:(1)由已知得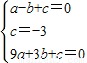 解得
解得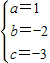 .
.
所以,抛物线的解析式为y=x2-2x-3.
(2)过D作DE⊥y轴于点E.
抛物线的解析式为y=x2-2x-3=(x-1)2-4,
则物线的顶点坐标为(1,-4),则OE=4,DE=1.
在直角△ODE中,根据勾股定理即可得到:OD=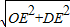 =
=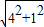 =
=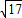 .
.
则sin∠BOD=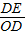 =
=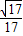 .
.
点评:主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.
(2)求出抛物线的顶点坐标,根据正弦函数的定义求解.
解答:
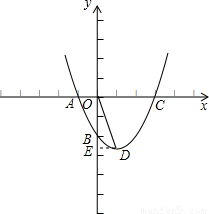 解:(1)由已知得
解:(1)由已知得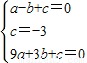 解得
解得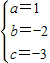 .
.所以,抛物线的解析式为y=x2-2x-3.
(2)过D作DE⊥y轴于点E.
抛物线的解析式为y=x2-2x-3=(x-1)2-4,
则物线的顶点坐标为(1,-4),则OE=4,DE=1.
在直角△ODE中,根据勾股定理即可得到:OD=
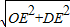 =
=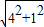 =
=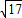 .
.则sin∠BOD=
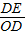 =
=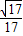 .
.点评:主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目