Question

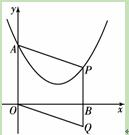
如图，平面直角坐标系中，抛物线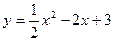交y轴于点A．P为抛物线
上一点，且与点A不重合．连结AP，以AO、AP为邻边作□OAPQ，PQ所在直线与x轴交
于点B．设点P的横坐标为．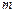
（1）点Q落在x轴上时m的值．（3分）
（3）若点Q在x轴下方，则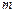为何值时，线段BQ的长取最大值，并求出这个最大值．（4分）[参考公式：二次函数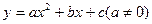的顶点坐标为（）]

Answer 1

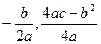解：（1）抛物线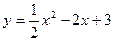与y轴交于点A，
∴点A的坐标为．∴OA=3．
∵四边形OAPQ为平行四边形，
∴QP=OA=3．
∴当点Q落在x轴上时，．
解得．
当m=0，点P与点A重合，不符合题意，舍去．
∴m=4．
（2）解法一：
∵点P的横坐标为m，
∴．
∴

．                                       （5分）
∵点Q在x轴下方，∴．
∴时，线段QB的长取最大值，最大值为2．                 (7分)
解法二：
∵QP =3，，
∴线段BP的长取最小值时，线段QB的长取最大值．
当点P为抛物线的顶点时，线段BP的长取最小值．
当时，．
∴线段BP的长最小值为1．                                    (5分)
∴时，线段QB的长取最大值，最大值为3－1=2．             (7分)

解析