题目内容
【题目】如图,在边长为2 ![]() 的正方形ABCD中,点E是CD边的中点,延长BC至点F,使CF=CE,连接BE,DF.将△BEC绕点C按顺时针方向旋转.当点E恰好落在DF上的点H处时,连接AG、DG、BG,则AG的长是.
的正方形ABCD中,点E是CD边的中点,延长BC至点F,使CF=CE,连接BE,DF.将△BEC绕点C按顺时针方向旋转.当点E恰好落在DF上的点H处时,连接AG、DG、BG,则AG的长是.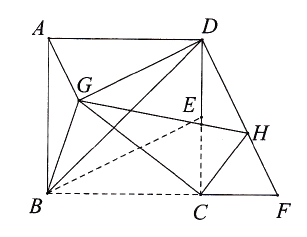
【答案】2
【解析】解:如图,过C作CK⊥DF于K,过H作HM⊥CF于M,过G作PN⊥BC,交AD于P,交BC于N,
∵CD=2 ![]() ,CE=CF=
,CE=CF= ![]() ,
,
∵四边形ABCD是正方形,
∴∠BCD=90°,
∴∠DCF=90°,
由勾股定理得:DF= ![]() ,
,
∵CK⊥DF,DC⊥CF,
∴∠FCK=∠CDF,
sin∠FCK=sin∠CDF= ![]() ,
,
∴ ![]() ,
,
∴FK=1,
∴CK= ![]() ,
,
由旋转得:CH=CE=CF,
∵CK⊥FH,
∴HF=2KF,
∴HF=2,
∴S△CHF= ![]() CFHM=
CFHM= ![]() HFCK,
HFCK,![]() HM=2×2,
HM=2×2,
HM= ![]() ,
,
∴CM= ![]() ,
,
∴tan∠HCF=  ,
,
设HM=4x,CM=3x,则CH=5x,
∵∠HCF=∠GCD=∠CGN,
∴cos∠CGN=cos∠HCF= ![]() =
= ![]() ,
,
∴GN= ![]() CG,
CG,
∵CG=BC=2 ![]() ,
,
∴GN= ![]() ×2
×2 ![]() =
= ![]() ,
,
∴NC= ![]() =
= ![]() ,
,
∴GP=2 ![]() -
- ![]() =
= ![]() ,
,
∴AP=BN=BC-NC=2 ![]() -
- ![]() =
= ![]() ,
,
由勾股定理得:AG= ![]()
![]() .
.
所以答案是:2.
【考点精析】本题主要考查了勾股定理的概念的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.

练习册系列答案
相关题目