题目内容
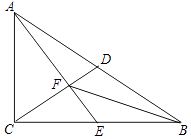
【题目】一张直角三角形纸片ABC,∠C=90°,AB=24,tanB= ![]() (如图),将它折叠使直角顶点C与斜边AB的中点重合,那么折痕的长为 .
(如图),将它折叠使直角顶点C与斜边AB的中点重合,那么折痕的长为 . 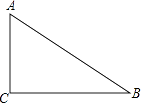
【答案】13
【解析】解:∵CD是斜边AB上的中线, ∴DC=DB= ![]() AB=12,
AB=12,
∴∠DCB=∠B,
由题意得,EF是CD的垂直平分线,
∴∠OEC+∠OCE=90°,又∠DCB+∠OCE=90°,
∴∠OEC=∠B,
设CF=2x,则CE=3x,
由勾股定理得,EF= ![]() x,
x,![]() ×2x×3x=
×2x×3x= ![]() ×
× ![]() x×6,
x×6,
解得,x= ![]() ,
,
∴EF= ![]() ×
× ![]() =13,
=13,
所以答案是:13.
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目