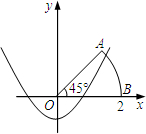
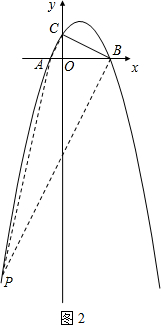
题目内容
二次函数y=一x2+ax+b图象与 轴交于
轴交于 ,
, 两点,且与
两点,且与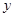 轴交于点
轴交于点 .
.
(1)则 的形状为 ;
的形状为 ;
(2)在此抛物线上一动点 ,使得以
,使得以 四点为顶点的四边形是梯形,则
四点为顶点的四边形是梯形,则 点的坐标为 .
点的坐标为 .
解析试题分析:(1)∵二次函数y=-x2+ax+b的图象经过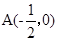 、B(2,0)两点,利用待定系数法就可以直接求出a、b的值,求出抛物线的解析式.
、B(2,0)两点,利用待定系数法就可以直接求出a、b的值,求出抛物线的解析式.
(2)在(1)题已将证得∠ACB=90°,若A、C、B、P四点为顶点的四边形是直角梯形,则有两种情况需要考虑:
①以BC、AP为底,AC为高;可先求出直线BC的解析式,进而可确定直线AP的解析式,联立抛物线的解析式即可求出点P的坐标.
②以AC、BP为底,BC为高;方法同①.
解:(1))∵二次函数y=-x2+ax+b的图象经过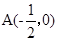 、B(2,0)两点,由题意,得
、B(2,0)两点,由题意,得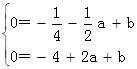 ,解得:
,解得: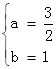 ,
,
∴抛物线的解析式为: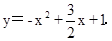
∴C(0,1),
∴ ,
,
CB2=BO2+CO2=5,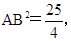 ,
,
∴AC2+CB2=AB2,
∴△ACB是直角三角形;
(2)存在,点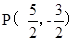 或
或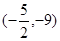 ;
;
若以A、C、B、P四点为顶点的直角梯形以BC、AP为底;
∵B(2,0),C(0,1),
∴直线BC的解析式为: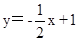 ;
;
设过点B且平行于AC的直线的解析式为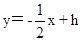 ,
,
将点 代入得:
代入得: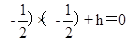 ,
,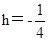 ;
;
∴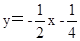 ;
;
联立抛物线的解析式有: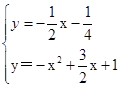 ,解得
,解得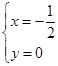 ,或
,或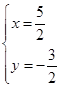 ;
;
∴点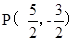 ;
;
若以A、C、B、P四点为顶点的直角梯形以AC、BP为底,
同理可求得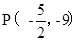 ;
;
故当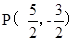 或
或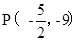 时,以A、C、B、P四点为顶点的四边形是直角梯形.
时,以A、C、B、P四点为顶点的四边形是直角梯形.
(根据抛物线的对称性求出另一个P点坐标亦可)
考点:二次函数综合题;待定系数法求二次函数解析式;二次函数与不等式(组);直角梯形.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目

 的图像至少有三个公共点,则实数b的取值范围 .
的图像至少有三个公共点,则实数b的取值范围 . 的顶点坐标是 .
的顶点坐标是 .
 的函数
的函数 与
与 的值为 .
的值为 .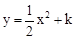 与扇形OAB的边界总有两个公共点,则实数k的取值范围是
与扇形OAB的边界总有两个公共点,则实数k的取值范围是