题目内容
已知:在△ABC中,AB=AC,∠B=30°,BC=6,点D在边BC上,点E在线段DC上,DE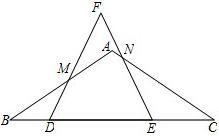 =3,△DEF是等边三角形,边DF、EF与边BA、CA分别相交于点M、N.
=3,△DEF是等边三角形,边DF、EF与边BA、CA分别相交于点M、N.(1)求证:△BDM∽△CEN;
(2)当点M、N分别在边BA、CA上时,设BD=x,△ABC与△DEF重叠部分的面积为y,求y关于x的函数解析式,并直接写出定义域;
(3)是否存在点D,使以M为圆心,BM为半径的圆与直线EF相切,如果存在,请求出x的值;如不存在,请说明理由.
分析:(1)两三角形中,AB=AC可得出∠B=∠C,三角形DEF是等边三角形可得出∠FDB=∠FEC=120°由此可证得两三角形相似.
(2)重合部分的面积应该是三角形ABC的面积-三角形BDM和CEN的面积和.那么要先求出三角形BDM和CEN的面积,由于∠B=∠C=30°,∠FDE=60°,∠BMD=∠C=30°,三角形BDM和BAC相似,那么可根据面积比等于相似比的平方用三角形ABC的面积求出三角形BDM的面积.同理可求出三角形CEN的面积,进而可得出重合部分的面积.
(3)如果存在EF于圆M相切的情况,那么如果过M作EF的垂线MG,那么MG=BM,可在三角形BDM中用BD来表示出BM,因为BD=DM,所以可以用BD表示出FM,进而在直角三角形FMG中表示出MG,然后让这两个含x的式子相等即可求出x的值.
(2)重合部分的面积应该是三角形ABC的面积-三角形BDM和CEN的面积和.那么要先求出三角形BDM和CEN的面积,由于∠B=∠C=30°,∠FDE=60°,∠BMD=∠C=30°,三角形BDM和BAC相似,那么可根据面积比等于相似比的平方用三角形ABC的面积求出三角形BDM的面积.同理可求出三角形CEN的面积,进而可得出重合部分的面积.
(3)如果存在EF于圆M相切的情况,那么如果过M作EF的垂线MG,那么MG=BM,可在三角形BDM中用BD来表示出BM,因为BD=DM,所以可以用BD表示出FM,进而在直角三角形FMG中表示出MG,然后让这两个含x的式子相等即可求出x的值.
解答:证明:(1)∵△ABC中,AB=AC,
∴∠B=∠C.
∵△DEF是等边三角形,
∴∠FDE=∠FED.
∴∠MDB=∠NEC.
∴△BDM∽△CEN.
(2)过A作AH⊥BC垂足为H,∵∠B=30°,BC=6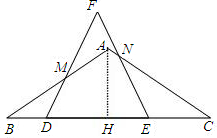 ,
,
∴BH=3,AH=
,AB=2
.
∴S△ABC=
×6×
=3
.
∵∠B=∠B,∠BMD=∠C,
∴△BDM∽△BAC.
∴
=(
)2,
=(
)2.
∴S△BDM=
x2同理求得S△NEC=
(3-x)2
∴y=3
-
x2-
(3-x)2=-
x2+
x+
(1≤x≤2).
(3)假设存在点D,使以M为圆心,BM为半径的圆与直线EF相切.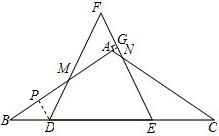
过点M作MG⊥EF垂足为G,则MG=BM,
在△BDM中,过点D作DP⊥BM垂足为P,
∵BD=x,∠B=30°,
∴BP=
x,BM=
x.
∵BD=DM,FD=DE=3,
∴FM=3-x.
∵在RT△FMG中,∠F=60°,
∴MG=
.
∴
x=
.
解得x=1.
所以当BD的长为1时,以M为圆心,BM为半径的圆与直线EF相切.
∴∠B=∠C.
∵△DEF是等边三角形,
∴∠FDE=∠FED.
∴∠MDB=∠NEC.
∴△BDM∽△CEN.
(2)过A作AH⊥BC垂足为H,∵∠B=30°,BC=6
 ,
,∴BH=3,AH=
| 3 |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 3 |
| 3 |
∵∠B=∠B,∠BMD=∠C,
∴△BDM∽△BAC.
∴
| S△BDM |
| S△ABC |
| BD |
| AB |
| S△BDM | ||
3
|
| x | ||
2
|
∴S△BDM=
| ||
| 4 |
| ||
| 4 |
∴y=3
| 3 |
| ||
| 4 |
| ||
| 4 |
| ||
| 2 |
3
| ||
| 2 |
3
| ||
| 4 |
(3)假设存在点D,使以M为圆心,BM为半径的圆与直线EF相切.

过点M作MG⊥EF垂足为G,则MG=BM,
在△BDM中,过点D作DP⊥BM垂足为P,
∵BD=x,∠B=30°,
∴BP=
| ||
| 2 |
| 3 |
∵BD=DM,FD=DE=3,
∴FM=3-x.
∵在RT△FMG中,∠F=60°,
∴MG=
| ||
| 2 |
∴
| 3 |
| ||
| 2 |
解得x=1.
所以当BD的长为1时,以M为圆心,BM为半径的圆与直线EF相切.
点评:本题主要考查了等边三角形的性质,切线的判定以及相似三角形的性质等知识点,运用好各特殊度数的角是解题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 25、已知:在△ABC中AB=AC,点D在CB的延长线上.
25、已知:在△ABC中AB=AC,点D在CB的延长线上. (1)化简:(a-
(1)化简:(a- 20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长.
20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长. 12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
 已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.
已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.