题目内容
设边长为3的正方形的对角线长为a．下列关于a的四种说法：①a是无理数；②a可以用数轴上的一个点来表示；③3＜a＜4；④a是18的算术平方根．其中，所有正确说法的序号是
- A.①④
- B.②③
- C.①②④
- D.①③④
C
分析：先利用勾股定理求出a=3
，再根据无理数的定义判断①；根据实数与数轴的关系判断②；利用估算无理数大小的方法判断③；利用算术平方根的定义判断④．
解答：∵边长为3的正方形的对角线长为a，
∴a=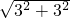
=
=3．
①a=3是无理数，说法正确；
②a可以用数轴上的一个点来表示，说法正确；
③∵16＜18＜25，4＜＜5，即4＜a＜5，说法错误；
④a是18的算术平方根，说法正确．
所以说法正确的有①②④．
故选C．
点评：本题主要考查了勾股定理，实数中无理数的概念，算术平方根的概念，实数与数轴的关系，估算无理数大小，有一定的综合性．
分析：先利用勾股定理求出a=3
，再根据无理数的定义判断①；根据实数与数轴的关系判断②；利用估算无理数大小的方法判断③；利用算术平方根的定义判断④．解答：∵边长为3的正方形的对角线长为a，
∴a=
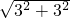==3．①a=3
是无理数，说法正确；②a可以用数轴上的一个点来表示，说法正确；
③∵16＜18＜25，4＜
＜5，即4＜a＜5，说法错误；④a是18的算术平方根，说法正确．
所以说法正确的有①②④．
故选C．
点评：本题主要考查了勾股定理，实数中无理数的概念，算术平方根的概念，实数与数轴的关系，估算无理数大小，有一定的综合性．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
设边长为2a的正方形的中心A在直线l上，它的一组对边垂直于直线l，半径为r的⊙O的圆心O在直线l上运动，点A、O间距离为d．
（1）如图①，当r＜a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：
所以，当r＜a时，⊙O与正方形的公共点的个数可能有 个；
（2）如图②，当r=a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：
所以，当r=a时，⊙O与正方形的公共点个数可能有 个；
（3）如图③，当⊙O与正方形有5个公共点时，试说明r=
a．
（1）如图①，当r＜a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：
| d、a、r之间的关系 | 公共点的个数 |
| d＞a+r | |
| d=a+r | |
| a-r＜d＜a+r | |
| d=a-r | |
| d＜a-r |
（2）如图②，当r=a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：
| d、a、r之间的关系 | 公共点的个数 |
| d＞a+r | |
| d=a+r | |
| a≤d＜a+r | |
| d＜a |
所以，当r=a时，⊙O与正方形的公共点个数可能有
（3）如图③，当⊙O与正方形有5个公共点时，试说明r=
| 5 |
| 4 |
