题目内容
【题目】比较下面每小题中两个算式结果的大小(在横线上填“>”、“<”或“=”).
⑴32+42 2×3×4;⑵22+22 2×2×2;⑶12+![]() 2×1×
2×1×![]() ;
;
⑷(-2) 2+52 2×(-2)×5;⑸![]()
![]()
通过观察上面的算式,请你用字母来表示上面算式中反映的一般规律.
【答案】(1)>(2)=(3)>(4)>(5)>; ![]() ≥2ab(当a=b时取等号).
≥2ab(当a=b时取等号).
【解析】试题分析:分别根据有理数的乘方法则求出各数的值,再根据有理数比较大小的法则比较出各数的大小,并总结出规律.
试题解析:(1)∵32+42=25,2×3×4=24,
∴32+42>2×3×4;
(2)∵22+22=8,2×2×2=8,
∴22+22=2×2×2;
(3)∵12+(![]() )2=
)2=![]() ,2×1×
,2×1×![]() =
=![]() =
=![]() ,
,
∴12+(![]() )2>2×1×
)2>2×1×![]() ;
;
(4)∵(-2)2+52=29,2×(-2)×5=-20,
∴(-2)2+52>2×(-2)×5;
(5)∵(![]() )2+(
)2+(![]() )2=
)2=![]() ,2×
,2×![]() ×
×![]() =
=![]() =
=![]() ,
,
∴(![]() )2+(
)2+(![]() )2>2×
)2>2×![]() ×
×![]() ,
,
故答案为:>,=,>,>,>,
用字母表示为:a2+b2≥2ab(当a=b时等号成立).

【题目】某校八年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
发言次数n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
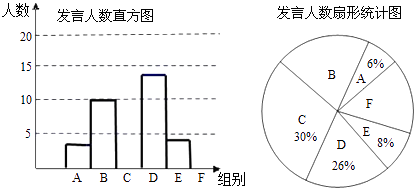
(1)求出样本容量,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天里发言次数不少于12次的人数;
(3)已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生.现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.



