题目内容
小乐发明了一个魔术盒,当任意有理数对(a,b)放入盒中,会得到一个新的有理数:a3+3a2b+3ab2+b3.例如:把(3,-2)放入其中,得到
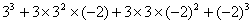 =19-18=1
=19-18=1
(1) 现将有理数对(-2,3)放入盒中的有理数m,在将有理数对(m,-7)放入盒中后得到的有理数是多少?
(2) 小乐现放入有理数对(2014,-2015),如果再现放入有理数对
(-2014,2015)那么两次得到的有理数会相等吗?请你说明理由。
(3) 依次放入有理数对(-2013, ),( ,2013)能使两次得到的有理数相等。
(4) 小乐先放入有理数对(m,n),请你放入有理数对( , ),让得到的有理数与小乐得到的有理数相等。
(1)将(-2,3)放入得:a3+3a2b+3ab2+b3=1,即m=1,
将(1,-7)放入即得:-216,;
(2) 两次得到的有理数相等。理由是:分别将两个有理数对代入得到算式一样。(计算过程,略)
(3) 依次放入有理数对(-2013,2012)与(-2014,2013)答案不唯一。
放入有理数对(n,m)使得到的有理数与小乐得到的有理数相等。

练习册系列答案
相关题目
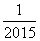

 ,其中x=2
,其中x=2 的相反数是 .
的相反数是 .
 55%)5% B、15×5%-15
55%)5% B、15×5%-15