题目内容
 如图,矩形ABCD中,AD=8,AB=9,AE=6,过D、E两点作直线L1与BC所在的直线L2交于点F.点O是直线L1与直线L2间的一动点,以O为圆心作⊙O,使⊙O与L1相切,又同时与矩形两边所在的直线相切,此时圆的半径是
如图,矩形ABCD中,AD=8,AB=9,AE=6,过D、E两点作直线L1与BC所在的直线L2交于点F.点O是直线L1与直线L2间的一动点,以O为圆心作⊙O,使⊙O与L1相切,又同时与矩形两边所在的直线相切,此时圆的半径是1或3
1或3
.分析:因为圆的位置不确定,所以需要分类讨论:①⊙O是△EFB的内切圆;②⊙O是△FCD的内切圆,再根据直角三角形的内切圆的半径为r=
计算即可.
| a+b+c |
| 2 |
解答: 解:∵矩形ABCD中,AD=8,AB=9,AE=6,
解:∵矩形ABCD中,AD=8,AB=9,AE=6,
∴BE=3,ED=10.
①如图1所示:
∵BE∥CD,
∴△FBE∽FCD,
∴
=
,
∴FB=4,
由勾股定理得:EF=5,
∴此时圆的半径是
=
=1;

②如图2所示:
FD=DE+EF=15,FC=FB+BC=4+8=12,CD=9,
∴此时圆的半径是
=
=3,
故答案为:1或3.
 解:∵矩形ABCD中,AD=8,AB=9,AE=6,
解:∵矩形ABCD中,AD=8,AB=9,AE=6,∴BE=3,ED=10.
①如图1所示:
∵BE∥CD,
∴△FBE∽FCD,
∴
| BE |
| CD |
| FB |
| FC |
∴FB=4,
由勾股定理得:EF=5,
∴此时圆的半径是
| a+b+c |
| 2 |
| 4+3-5 |
| 2 |

②如图2所示:
FD=DE+EF=15,FC=FB+BC=4+8=12,CD=9,
∴此时圆的半径是
| a+b+c |
| 2 |
| 12+9-15 |
| 2 |
故答案为:1或3.
点评:本题考查了矩形的性质、勾股定理的运用、相似三角形的判定和性质以及直角三角形内切圆的半径和三边的数量关系,题目的综合性不小,并且注意分类讨论思想的运用.

练习册系列答案
相关题目
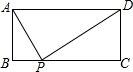 如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )
如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )A、a≥
| ||
| B、a≥b | ||
C、a≥
| ||
| D、a≥2b |
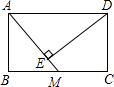 如图,矩形ABCD中,AB=6,BC=8,M是BC的中点,DE⊥AM,E是垂足,则△ABM的面积为
如图,矩形ABCD中,AB=6,BC=8,M是BC的中点,DE⊥AM,E是垂足,则△ABM的面积为 7、如图,矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,则∠CAE=
7、如图,矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,则∠CAE= (2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为
(2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为 (2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.
(2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.