Question

已知：如图，在平面直角坐标系xOy中，直线AB与x轴、y轴的交点分别为A、B，OB=3，tan∠OAB=

3

4

，将∠OBA对折，使点O的对应点H恰好落在直线AB上，折痕交x轴于点C，
（1）求过A、B、C三点的抛物线解析式；
（2）若抛物线的顶点为D，在直线BC上是否存在点P，使得四边形ODAP为平行四边形？若存在，求出点P的坐标；若不存在，说明理由；
（3）若点Q是抛物线上一个动点，使得以A、B、Q为顶点并且以AB为直角边的直角三角形，直接写出Q点坐标．

Answer 1

分析：（1）欲求抛物线的解析式，需用待定系数法，那么就必须首先求出A、B、C三点的坐标；已知OB的长，在Rt△AOB中，根据∠OAB的正切值即可得到OA的长，则A、B点的坐标可得；连接CH，根据题意不难看出点O、H关于直线BC对称，所以OC=CH、BH=BO，设出点C的坐标，然后用其横坐标表达出OC、CH、AH的长，在Rt△ACH中，根据勾股定理即可确定点C的坐标；所有条件已求得，则题目可解．
（2）将（1）的抛物线解析式写成顶点式，则点D的坐标可得；若四边形ADAP是符合条件的平行四边形，根据图示可以看出，只有OA作对角线，那么P、D关于线段OA的中点对称，可据此先得到点P的坐标，然后代入直线BC的解析式中进行验证．
（3）AB为Rt△ABQ的直角边，那么点B或点A应为直角三角形的直角顶点，即直线BQ（或直线AQ）、直线AB的斜率乘积为-1，首先求出直线AB的解析式，在确定出直线BQ（或直线AQ）的斜率后，代入点B（点A）的坐标，求出直线BQ（或直线AQ）的解析式，联立抛物线的解析式后即可求出点Q的坐标．

解答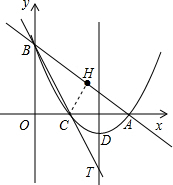：解：（1）∵在Rt△BOA中，OB=3，tan∠OAB=

3

4

，
∴OA=4，AB=5，
∴A（4，0），B（0，3）
设C（m，0），连接CH，如图，由对称性知，CH=OC=m，BH=BO=3，∠BHC=∠BOC=90°，
∴AH=AB-BH=2，AC=4-m，
∴在Rt△CHA中，由CH²+AH²=AC²，即 m²+2²=（4-m）²，得：m=

3

2

，
∴C（

3

2

，0）
设过A、B、C三点的抛物线的解析式为 y=a（x-

3

2

）（x-4），将x=0，y=3代入抛物线的解析式，得 a=

1

2

，
∴y=

1

2

（x-

3

2

）（x-4）=

1

2

x²-

11

4

x+3，
即过A、B、C三点的抛物线的解析式为 y=

1

2

x²-

11

4

x+3．

（2）y=

1

2

x²-

11

4

x+3=

1

2

（x-

11

4

）²-

25

32

，
∴抛物线的对称轴为直线 x=

11

4

，顶点D的坐标为（

11

4

，-

25

32

），
由B（0，3），C（

3

2

，0）可求得直线BC的解析式：y=-2x+3．
由图示知，若点P在直线BC上，且四边形OPAD是平行四边形，只有OP

∥

.

AD一种情况，此时D、P关于线段OA的中点对称；
由A（4，0）知，OA的中点（2，0），则P（

5

4

，

25

32

）；
当x=

5

4

时，y=-2x+3=-2×

5

4

+3=

1

2

≠

25

32

，所以点P不在直线BC上，与题意不合；
∴直线BC上不存在符合题意的点P，使得四边形ODAP为平行四边形．

（3）由A（4，0）、B（0，3）可得，直线AB：y=-

3

4

x+3；
取直线l⊥AB，则 k_l•k_AB=-1，即 k_l=

4

3

，可设直线l：y=

4

3

x+b；
①当直线l过点B时，直线l与抛物线的交点为点Q；
将B（0，3）代入y=

4

3

x+b中，得：b=3，
即直线l：y=

4

3

x+3，联立抛物线的解析式，得：

y= 4 3 x+3 y= 1 2 x2- 11 4 x+3

，解得

x1=0 y1=3

、

x2= 49 6 y2= 125 9

∴Q₁（

49

6

，

125

9

）；
②当直线l过点A时，直线l与抛物线的交点为点Q；
同①可求得：Q₂（

25

6

，

2

9

）；
综上，得：Q₁（

49

6

，

125

9

）、Q₂（

25

6

，

2

9

）．

点评：此题主要考查了二次函数解析式的确定、勾股定理的应用、平行四边形的性质和判定、直角三角形的判定、垂直直线间的斜率关系等综合知识；（2）题中，根据图示先确定点P的位置可以大大的减少计算量；（3）题中，以AB为直角边包括了A、B分别为直角顶点两种情况，应分类进行讨论．