Question

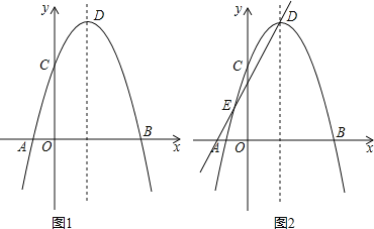
【题目】如图1，在平面直角坐标系xOy中，抛物线y=-（x-a）（x-4）（a＜0）与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，点D为抛物线的顶点．

（1）若D点坐标为（），求抛物线的解析式和点C的坐标；

（2）若点M为抛物线对称轴上一点，且点M的纵坐标为a，点N为抛物线在x轴上方一点，若以C、B、M、N为顶点的四边形为平行四边形时，求a的值；

（3）直线y=2x+b与（1）中的抛物线交于点D、E（如图2），将（1）中的抛物线沿着该直线方向进行平移，平移后抛物线的顶点为D′，与直线的另一个交点为E′，与x轴的交点为B′，在平移的过程中，求D′E′的长度；当∠E′D′B′=90°时，求点B′的坐标．

Answer 1

【答案】（1）y=-x2+3x+4，C（0，4）；（2）a1=-2-2，a2=；（3）D′E′=2，B′（-1，0）．

【解析】

（1）将点D的坐标代入函数解析式，求得a的值；利用抛物线解析式来求点C的值．
（2）需要分类讨论：BC为边和BC为对角线两种情况，根据“平行四边形的对边平行且相等，平行四边形的对角线相互平分”的性质列出方程组，利用方程思想解答．
（3）根据平移规律得到D′E′的长度、平移后抛物线的解析式，然后由函数图象上点的坐标特征求得点B′的坐标．

（1）依题意得：=-（-a）（-4）．

解得a=-1．

∴抛物线解析式为：y=-（x+1）（x-4）或y=-x2+3x+4．

∴C（0，4）．

（2）由题意知：A（a，0），B（4，0），C（0，-4a）．

对称轴为直线x=，则M（，a）．

①MN∥BC且MN=BC，根据点的平移特征可知N（，-3a）．

则-3a=-（-a）（-4）．

解得：a=-2±2（舍去正值）．

②当BC为对角线时，设N（x，y）．

根据平行四边形的对角线互相平分可得：．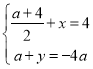

解得．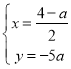

则-5a=-（-a）（-4）．

解得a=．（舍去正值）

∴a1=-2-2，a2=．

（3）把D（）代入y=2x+b得到：2×+b=．则b=．

故直线解析式为：y=2x+．

联立．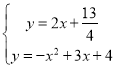

解得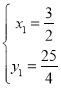（舍去），．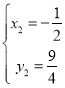

∴E（-，）

∴DE=2．

根据抛物线的平移规律，则平移后线段D′E′始终等于2．

设平移后的D′（m，2m+），则E′（m-2，2m-）．

平移后抛物线的解析式为：y=-（x-m）2+2m+．

则D′B′：y=-x+n过点（m，2m+），

∴y=-x+m+，则B′（5m+，0）．

∴-（5m+）+m+=0．

解得m1=-，m2=-．

∴B′1（-1，0），B′2（-，0）（与D′重合，舍去）．

综上所述，B′（-1，0）．