题目内容
已知函数y=2x2-4mx+m2的图象与x轴交于A、B两点,顶点为C,若△ABC的面积为4
,那么m=
| 2 |
±2
±2
.分析:利用根与系数的关系求出AB的长度,再根据顶点左边求出顶点C到x轴的距离,然后根据△ABC的面积列式求解,再根据立方根的定义即可求出m的值.
解答:解:设2x2-4mx+m2=0的两个根是x1,x2,
则x1+x2=-
=-
=2m,
x1•x2=
=
,
∴AB=|x1-x2|=
=|
m|,
点C到x轴的距离是:|
|=|
|=m2,
∴△ABC的面积=
×|
m|×m2=4
,
解得|m|3=8,
∴m=±2.
故答案为:±2.
则x1+x2=-
| b |
| a |
| -4m |
| 2 |
x1•x2=
| c |
| a |
| m2 |
| 2 |
∴AB=|x1-x2|=
| ( x1+x2)2-4x1x2 |
| 2 |
点C到x轴的距离是:|
| 4ac-b2 |
| 4a |
| 4×2×m2-(-4m)2 |
| 4×2 |
∴△ABC的面积=
| 1 |
| 2 |
| 2 |
| 2 |
解得|m|3=8,
∴m=±2.
故答案为:±2.
点评:本题考查了抛物线与x轴的交点问题,根据根与系数的关系表示出AB的长度是解题的关键,难度中等.

练习册系列答案
相关题目
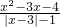 的值为零,求x的值.
的值为零,求x的值. 有实根.
有实根. ,求k的值.
,求k的值.